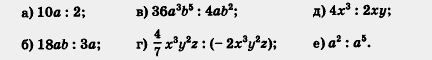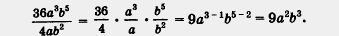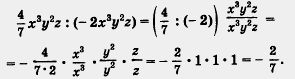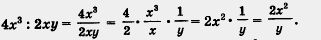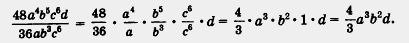|
|
|
| (6 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Умножение одночленов. Возведение одночлена в натуральную степень</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Умножение одночленов, Возведение одночлена в натуральную степень, дроби, степень, натуральное число</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Умножение одночленов. Возведение одночлена в натуральную степень''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Умножение одночленов. Возведение одночлена в натуральную степень''' |
| Строка 7: |
Строка 7: |
| | <br> | | <br> |
| | | | |
| - | '''ДЕЛЕНИЕ ОДНОЧЛЕНА НА ОДНОЧЛЕН '''
| + | '''Деление одночлена на одночлен''' |
| | | | |
| - | <br>Что такое одночлен, мы знаем; как одночлены складывать, вычитать, перемножать и даже возводить в степень, обсудили. Но ведь имеется еще одна арифметическая операция — деление. Вот об этом и поговорим. <br><u>Пример 1.</u> Опираясь на свойства арифметических действий, попытаемся выполнить деление одночленов:
| + | Что такое '''[[Одночлен. Піднесення одночленів до степеня. Множення одночленів|одночлен]]''', мы знаем; как одночлены складывать, вычитать, перемножать и даже возводить в степень, обсудили. Но ведь имеется еще одна арифметическая операция — деление. Вот об этом и поговорим. <br><u>Пример 1.</u> Опираясь на свойства арифметических действий, попытаемся выполнить деление одночленов: |
| | | | |
| - | [[Image:07-06-128.jpg]]<br>Решение,
| + | <br> |
| | | | |
| - | а) Воспользуемся тем, что если произведение двух чисел делят на третье число, то можно разделить на это число один из множителей <br>и полученное частное умножить на другой множитель. (Вспомнили? Например, 10a:3 = (12:3) • 4= 4• 4 = 16<br> Имеем: <br>10a:2 =( 10:2)• a = 5a. <br>б) Рассуждая, как и в примере а), получаем:
| + | [[Image:07-06-128.jpg|480px|Деление одночленов]] |
| | | | |
| - | 18ab: 3a =(18 :3) •(a: a)b =6•1•b =6b<br>в) 36a<sup>3</sup>b<sup>5</sup> : 4ab<sup>2</sup> = (36 : 4)-(a<sup>3</sup> : a)•(b<sup>5</sup> : b<sup>2</sup>) = 9a<sup>3-1</sup> • b<sup>5</sup><sup>-2</sup> = = 9a<sup>2</sup>b<sup>3</sup>. <br>Иногда удобнее вместо знака деления (:) использовать черту дроби. Вот как тогда будет выглядеть решение примера в):
| + | <br>Решение, |
| | | | |
| - | [[Image:07-06-129.jpg]]<br><br>г) Здесь мы используем комбинированную запись решения, т. е. и знак деления, и черту дроби:
| + | а) Воспользуемся тем, что если произведение двух чисел делят на третье число, то можно разделить на это число один из множителей и полученное частное умножить на другой множитель. (Вспомнили? |
| | | | |
| - | [[Image:07-06-130.jpg]]<br><br>Здесь все верно, но, как говорят математики, нерационально, поскольку сразу было ясно, что х3у2г : х3у2г = 1 (фактически выражение делится само на себя). <br>д) [[Image:07-06-131.jpg]]<br>Это не одночлен, значит, разделить 4x<sup>3</sup> на 2ху нельзя (в том смысле, чтобы в частном получился одночлен).
| + | Например, 10a:3 = (12:3) • 4= 4• 4 = 16 |
| | | | |
| - | е) И эта задача невыполнима, так как мы пока не умеем делить при одном и том же основании степень с меньшим показателем на степень с большим показателем. <br>Мы рассмотрели шесть примеров, из них четыре оказались корректными, а два (последние) — некорректными (этот термин мы ввели в § 11). <br>Проанализируем теперь решенные примеры и попробуем с помощью этого анализа выяснить, когда можно разделить одночлен на одночлен так, чтобы в частном снова получился одночлен. | + | Имеем: |
| | + | |
| | + | 10a:2 =( 10:2)• a = 5a. |
| | + | |
| | + | <br>б) Рассуждая, как и в примере а), получаем: |
| | + | |
| | + | 18ab: 3a =(18 :3) •(a: a)b =6•1•b =6b |
| | + | |
| | + | <br>в) 36a<sup>3</sup>b<sup>5</sup> : 4ab<sup>2</sup> = (36 : 4)-(a<sup>3</sup> : a)•(b<sup>5</sup> : b<sup>2</sup>) = 9a<sup>3-1</sup> • b<sup>5</sup><sup>-2</sup> = = 9a<sup>2</sup>b<sup>3</sup>. |
| | + | |
| | + | <br>Иногда удобнее вместо знака деления (:) использовать черту '''[[Основное свойство алгебраической дроби|дроби]]'''. Вот как тогда будет выглядеть решение примера в): |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:07-06-129.jpg|480px|Решение примера]]<br><br>г) Здесь мы используем комбинированную запись решения, т. е. и знак деления, и черту дроби: |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:07-06-130.jpg|480px|Комбинированая запись решения]]<br><br>Здесь все верно, но, как говорят математики, нерационально, поскольку сразу было ясно, что х3у2г : х3у2г = 1 (фактически выражение делится само на себя). |
| | + | |
| | + | д) |
| | + | |
| | + | [[Image:07-06-131.jpg|480px|Решение примера]] |
| | + | |
| | + | <br>Это не одночлен, значит, разделить 4x<sup>3</sup> на 2ху нельзя (в том смысле, чтобы в частном получился одночлен). |
| | + | |
| | + | е) И эта задача невыполнима, так как мы пока не умеем делить при одном и том же основании степень с меньшим показателем на '''[[Вирази зі степенями. Вправи та задачі|степень]]''' с большим показателем. |
| | + | |
| | + | Мы рассмотрели шесть примеров, из них четыре оказались корректными, а два (последние) — некорректными (этот термин мы ввели в § 11). |
| | + | |
| | + | Проанализируем теперь решенные примеры и попробуем с помощью этого анализа выяснить, когда можно разделить одночлен на одночлен так, чтобы в частном снова получился одночлен. |
| | | | |
| | ''Первое наблюдение.'' Оба одночлена (и делимое, и делитель) должны быть записаны в стандартном виде (впрочем, об этом мы условились еще в § 10). | | ''Первое наблюдение.'' Оба одночлена (и делимое, и делитель) должны быть записаны в стандартном виде (впрочем, об этом мы условились еще в § 10). |
| Строка 31: |
Строка 61: |
| | ''Четвертое наблюдение. ''Коэффициенты делимого и делителя могут быть любыми (поскольку мы умеем делить друг на друга любые числа, кроме, разумеется, деления на нуль). | | ''Четвертое наблюдение. ''Коэффициенты делимого и делителя могут быть любыми (поскольку мы умеем делить друг на друга любые числа, кроме, разумеется, деления на нуль). |
| | | | |
| - | Значит, если вам предложат разделить одночлен на одночлен, то сначала убедитесь, что задача корректна, т. е. проведите указанные наблюдения и <br>убедитесь, что все в порядке. В случае, когда задача корректна, решайте ее по образцу примера 1. | + | Значит, если вам предложат разделить одночлен на одночлен, то сначала убедитесь, что задача корректна, т. е. проведите указанные наблюдения и убедитесь, что все в порядке. В случае, когда задача корректна, решайте ее по образцу примера 1. |
| | | | |
| | <u>Пример 2. </u>Упростить 48a<sup>4</sup>b<sup>5</sup>c<sup>6</sup>d : 36ab<sup>3</sup>c<sup>6</sup>. <br>Р е ш е н и е. | | <u>Пример 2. </u>Упростить 48a<sup>4</sup>b<sup>5</sup>c<sup>6</sup>d : 36ab<sup>3</sup>c<sup>6</sup>. <br>Р е ш е н и е. |
| Строка 37: |
Строка 67: |
| | 1) Оба одночлена (и делимое, и делитель) записаны в стандартном виде. | | 1) Оба одночлена (и делимое, и делитель) записаны в стандартном виде. |
| | | | |
| - | 2) В делимом фигурируют переменные а, Ъ, с, d, в делителе а, Ъ, с. Лишних переменных в делителе нет. | + | 2) В делимом фигурируют переменные а, b, с, d, в делителе а, b, с. Лишних переменных в делителе нет. |
| | | | |
| | 3) В делителе нет степеней больших, чем у одноименных переменных в делимом. | | 3) В делителе нет степеней больших, чем у одноименных переменных в делимом. |
| | | | |
| - | Вывод: задача корректна, будем ее решать. <br>Имеем: | + | Вывод: задача корректна, будем ее решать. |
| | | | |
| - | [[Image:07-06-132.jpg]]<br><br>Вы чувствуете, что в § 12, как и в § 10, есть недоговоренность? А что же все-таки делать, если одночлен на одночлен не разделился? Разве мы застрахованы от такой ситуации? Поэтому математики ввели новый объект — алгебраическую дробь (вспомните, ведь и обыкновенные дроби появились <br>из-за того, что не любые два натуральных числа делятся друг на друга; например, 14 делится на 7, а 3 не делится на 7. Как записывается ответ во втором случае? Он записывается в виде обыкновенной дроби [[Image:07-06-133.jpg]]. Такая алгебраическая дробь встретилась нам ранее, в примере 1д) — это было выражение [[Image:07-06-134.jpg]] И, конечно, математики научились оперировать с этими новыми объектами — алгебраическими дробями. Мы будем изучать их в курсе алгебры 8 класса. <br><br>
| + | <br>Имеем: |
| | | | |
| | <br> | | <br> |
| | + | |
| | + | [[Image:07-06-132.jpg|480px|Решение примера]]<br><br>Вы чувствуете, что в § 12, как и в § 10, есть недоговоренность? А что же все-таки делать, если одночлен на одночлен не разделился? Разве мы застрахованы от такой ситуации? Поэтому математики ввели новый объект — алгебраическую '''[[Основное свойство алгебраической дроби|дробь]]''' (вспомните, ведь и обыкновенные дроби появились из-за того, что не любые два '''[[Додавання і віднімання натуральних чисел|натуральных числа]]''' делятся друг на друга; например, 14 делится на 7, а 3 не делится на 7. Как записывается ответ во втором случае? Он записывается в виде обыкновенной дроби [[Image:07-06-133.jpg|30px|Обыкновенная дробь]]. Такая алгебраическая дробь встретилась нам ранее, в примере 1д) — это было выражение [[Image:07-06-134.jpg|40px|Выражение]] И, конечно, математики научились оперировать с этими новыми объектами — алгебраическими дробями. Мы будем изучать их в курсе алгебры 8 класса. <br><br> |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <sub>Библиотека с учебниками и книгами на скачку бесплатно [[Гипермаркет знаний - первый в мире!|онлайн]], Математика для 7 класса [[Математика|скачать]], школьная программа по математике, планы конспектов уроков </sub> | + | <br> |
| | + | |
| | + | <sub>Библиотека для [http://xvatit.com/vuzi/ '''ВУЗов'''] с учебниками и книгами на скачку бесплатно [[Гипермаркет знаний - первый в мире!|онлайн]], Математика для 7 класса [[Математика|скачать]], школьная программа по математике, планы конспектов уроков </sub> |
| | + | |
| | + | <sub></sub> |
| | + | |
| | + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 19:03, 14 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Умножение одночленов. Возведение одночлена в натуральную степень
Деление одночлена на одночлен
Что такое одночлен, мы знаем; как одночлены складывать, вычитать, перемножать и даже возводить в степень, обсудили. Но ведь имеется еще одна арифметическая операция — деление. Вот об этом и поговорим.
Пример 1. Опираясь на свойства арифметических действий, попытаемся выполнить деление одночленов:
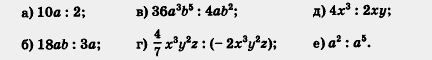
Решение,
а) Воспользуемся тем, что если произведение двух чисел делят на третье число, то можно разделить на это число один из множителей и полученное частное умножить на другой множитель. (Вспомнили?
Например, 10a:3 = (12:3) • 4= 4• 4 = 16
Имеем:
10a:2 =( 10:2)• a = 5a.
б) Рассуждая, как и в примере а), получаем:
18ab: 3a =(18 :3) •(a: a)b =6•1•b =6b
в) 36a3b5 : 4ab2 = (36 : 4)-(a3 : a)•(b5 : b2) = 9a3-1 • b5-2 = = 9a2b3.
Иногда удобнее вместо знака деления (:) использовать черту дроби. Вот как тогда будет выглядеть решение примера в):
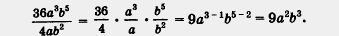
г) Здесь мы используем комбинированную запись решения, т. е. и знак деления, и черту дроби:
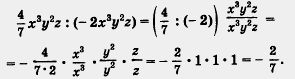
Здесь все верно, но, как говорят математики, нерационально, поскольку сразу было ясно, что х3у2г : х3у2г = 1 (фактически выражение делится само на себя).
д)
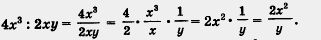
Это не одночлен, значит, разделить 4x3 на 2ху нельзя (в том смысле, чтобы в частном получился одночлен).
е) И эта задача невыполнима, так как мы пока не умеем делить при одном и том же основании степень с меньшим показателем на степень с большим показателем.
Мы рассмотрели шесть примеров, из них четыре оказались корректными, а два (последние) — некорректными (этот термин мы ввели в § 11).
Проанализируем теперь решенные примеры и попробуем с помощью этого анализа выяснить, когда можно разделить одночлен на одночлен так, чтобы в частном снова получился одночлен.
Первое наблюдение. Оба одночлена (и делимое, и делитель) должны быть записаны в стандартном виде (впрочем, об этом мы условились еще в § 10).
Второе наблюдение. В делителе не должно быть переменных, которых нет в делимом (по этой причине мы «споткнулись»
Третье наблюдение. Если в делимом и делителе есть одна и та же переменная, причем в делимом она возводится в степень n, а в делителе — в степень k, то число k не должно быть больше числа n (поэтому мы «споткнулись» в примере 1е).
Четвертое наблюдение. Коэффициенты делимого и делителя могут быть любыми (поскольку мы умеем делить друг на друга любые числа, кроме, разумеется, деления на нуль).
Значит, если вам предложат разделить одночлен на одночлен, то сначала убедитесь, что задача корректна, т. е. проведите указанные наблюдения и убедитесь, что все в порядке. В случае, когда задача корректна, решайте ее по образцу примера 1.
Пример 2. Упростить 48a4b5c6d : 36ab3c6.
Р е ш е н и е.
1) Оба одночлена (и делимое, и делитель) записаны в стандартном виде.
2) В делимом фигурируют переменные а, b, с, d, в делителе а, b, с. Лишних переменных в делителе нет.
3) В делителе нет степеней больших, чем у одноименных переменных в делимом.
Вывод: задача корректна, будем ее решать.
Имеем:
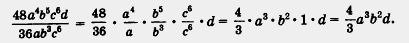
Вы чувствуете, что в § 12, как и в § 10, есть недоговоренность? А что же все-таки делать, если одночлен на одночлен не разделился? Разве мы застрахованы от такой ситуации? Поэтому математики ввели новый объект — алгебраическую дробь (вспомните, ведь и обыкновенные дроби появились из-за того, что не любые два натуральных числа делятся друг на друга; например, 14 делится на 7, а 3 не делится на 7. Как записывается ответ во втором случае? Он записывается в виде обыкновенной дроби 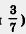 . Такая алгебраическая дробь встретилась нам ранее, в примере 1д) — это было выражение . Такая алгебраическая дробь встретилась нам ранее, в примере 1д) — это было выражение 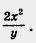 И, конечно, математики научились оперировать с этими новыми объектами — алгебраическими дробями. Мы будем изучать их в курсе алгебры 8 класса. И, конечно, математики научились оперировать с этими новыми объектами — алгебраическими дробями. Мы будем изучать их в курсе алгебры 8 класса.
Библиотека для ВУЗов с учебниками и книгами на скачку бесплатно онлайн, Математика для 7 класса скачать, школьная программа по математике, планы конспектов уроков
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|