|
|
|
| (5 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Вынесение общего множителя за скобки</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Вынесение общего множителя за скобки, многочлен? степень, одночлен, алгебраическое выражение</metakeywords> |
| | | | |
| | <br> '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Вынесение общего множителя за скобки''' | | <br> '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Вынесение общего множителя за скобки''' |
| | | | |
| - | <br> ''' Вынесение общего множителя за скобки'''<br> | + | <br> ''' '''[[Вынесение общего множителя за скобки. Задачи|'''Вынесение общего множителя за скобки''']]'''<br> ''' |
| | | | |
| - | <br>Прежде чем начинать изучение этого параграфа, вернитесь к § 15. Там мы уже рассмотрели пример, в котором требоk валось представить многочлен в виде произведения многочлена и одночлена. Мы установили, что эта задача не всегда корректна. Если все же такое про? изведение удалось составить, то обычно говорят, вынесение что многочлен разложен на множители с помощью общего вынесения общего множителя за скобки. Рассмотрим несколько примеров.
| + | Прежде чем начинать изучение этого параграфа, вернитесь к § 15. Там мы уже рассмотрели пример, в котором требовалось представить '''[[Розклад многочленів на множники. Винесення спільного множника за дужки. Задачі та вправи|многочлен]]''' в виде произведения многочлена и одночлена. Мы установили, что эта задача не всегда корректна. Если все же такое произведение удалось составить, то обычно говорят, вынесение что многочлен разложен на множители с помощью общего вынесения общего множителя за скобки. Рассмотрим несколько примеров. |
| | | | |
| | <br> '''Пример 1.''' Разложить на множители многочлен: | | <br> '''Пример 1.''' Разложить на множители многочлен: |
| Строка 13: |
Строка 13: |
| | б) а<sup>3</sup> + а<sup>2</sup> = а<sup>2</sup>(а + 1). Если одна и та же переменная входит во все члены многочлена, то ее можно вынести за скобки в степени, равной наименьшей из имеющихся (т. е. выбирают наименьший из имеющихся показателей).<br> | | б) а<sup>3</sup> + а<sup>2</sup> = а<sup>2</sup>(а + 1). Если одна и та же переменная входит во все члены многочлена, то ее можно вынести за скобки в степени, равной наименьшей из имеющихся (т. е. выбирают наименьший из имеющихся показателей).<br> |
| | | | |
| - | в) Здесь используем тот же прием, что и при решении примеров а) и б): для коэффициентов находим общий делитель (в данном случае число 2), для переменных — наименьшую степень из имеющихся (в данном случае а<sup>2</sup>). Получаем: <br> | + | в) Здесь используем тот же прием, что и при решении примеров а) и б): для коэффициентов находим общий делитель (в данном случае число 2), для переменных — наименьшую '''[[Свойства степени с натуральным показателем|степень]]''' из имеющихся (в данном случае а<sup>2</sup>). Получаем: <br> |
| | | | |
| | 4а<sup>3</sup> + 6а<sup>2</sup> = 2а<sup>2</sup> • 2а + 2а<sup>2</sup> • 3 = 2а<sup>2</sup> (2а + 3).<br> | | 4а<sup>3</sup> + 6а<sup>2</sup> = 2а<sup>2</sup> • 2а + 2а<sup>2</sup> • 3 = 2а<sup>2</sup> (2а + 3).<br> |
| | | | |
| - | г) Обычно для целочисленных коэффициентов стараются найти не просто общий делитель, а наибольший общий делитель. Для коэффициентов 12 и 18 им будет число 6. Замечаем, что переменная а входит в оба члена многочлена, при этом наименьший показапоказатель равен 1. Переменная Ь также входит в оба члена многочлена, причем наименьший показатель равен 3. Наконец, переменная с входит только во второй член многочлена и не входит в первый член, значит, эту переменную нельзя вынести за скобки ни в какой степени. В итоге имеем:<br> | + | г) Обычно для целочисленных коэффициентов стараются найти не просто общий делитель, а наибольший общий делитель. Для коэффициентов 12 и 18 им будет число 6. Замечаем, что переменная а входит в оба члена многочлена, при этом наименьший показапоказатель равен 1. Переменная b также входит в оба члена многочлена, причем наименьший показатель равен 3. Наконец, переменная с входит только во второй член многочлена и не входит в первый член, значит, эту переменную нельзя вынести за скобки ни в какой степени. В итоге имеем:<br> |
| | | | |
| | 12аb<sup>4</sup> - 18а<sup>2</sup>Ь<sup>3</sup>с = 6аЬ<sup>3</sup> • 2b - 6аЬ<sup>3</sup> • Зас = 6аb<sup>3</sup>(2b - Зас).<br> | | 12аb<sup>4</sup> - 18а<sup>2</sup>Ь<sup>3</sup>с = 6аЬ<sup>3</sup> • 2b - 6аЬ<sup>3</sup> • Зас = 6аb<sup>3</sup>(2b - Зас).<br> |
| Строка 45: |
Строка 45: |
| | Получим: <br>-х<sup>4</sup>у<sup>3</sup> -2х<sup>3</sup>у<sup>2</sup>+ 5х<sup>2 </sup>= - х<sup>2</sup>(х<sup>2</sup> у<sup>3</sup> + 2ху<sup>2</sup> - 5). | | Получим: <br>-х<sup>4</sup>у<sup>3</sup> -2х<sup>3</sup>у<sup>2</sup>+ 5х<sup>2 </sup>= - х<sup>2</sup>(х<sup>2</sup> у<sup>3</sup> + 2ху<sup>2</sup> - 5). |
| | | | |
| - | '''Пример 3'''. Можно ли разделить многочлен 5а<sup>4</sup> - 10а<sup>3</sup> + 15а<sup>5</sup> на одночлен 5а<sup>3</sup>? Если да, то выполнить деление. | + | '''Пример 3'''. Можно ли разделить многочлен 5а<sup>4</sup> - 10а<sup>3</sup> + 15а<sup>5</sup> на одночлен 5а<sup>3</sup>? Если да, то выполнить '''[[Умножение и деление степеней с одинаковыми показателями|деление]]'''. |
| | | | |
| | Решение. В примере 1д) мы получили, что | | Решение. В примере 1д) мы получили, что |
| Строка 55: |
Строка 55: |
| | Подобные примеры мы рассматривали в § 18; просмотрите их, пожалуйста, еще раз, но уже с точки зрения вынесения общего множителя за скобки. | | Подобные примеры мы рассматривали в § 18; просмотрите их, пожалуйста, еще раз, но уже с точки зрения вынесения общего множителя за скобки. |
| | | | |
| - | Разложение многочлена на множители с помо щью вынесения общего множителя за скобки тесно связано с двумя операциями, которые мы изучали в § 15 и 18, — с умножением многочлена на одночлен и с делением многочлена на одночлен.
| + | Разложение многочлена на множители с помощью вынесения общего множителя за скобки тесно связано с двумя операциями, которые мы изучали в § 15 и 18, — с умножением многочлена на одночлен и с делением многочлена на '''[[Одночлен. Піднесення одночленів до степеня. Множення одночленів|одночлен]]'''. |
| | | | |
| - | А теперь несколько расширим наши представления о вынесении общего множителя за скобки. Дело в том, что иногда алгебраическое выражение задается в таком виде, что в качестве общего множителя может выступать не одночлен, а сумма нескольких одночленов. | + | А теперь несколько расширим наши представления о вынесении общего множителя за скобки. Дело в том, что иногда '''[[Основное свойство алгебраической дроби|алгебраическое выражение]]''' задается в таком виде, что в качестве общего множителя может выступать не одночлен, а сумма нескольких одночленов. |
| | | | |
| | '''Пример 4.''' Разложить на множители: | | '''Пример 4.''' Разложить на множители: |
| Строка 73: |
Строка 73: |
| | у(2х + 5у) = (х- 2)(2x + 5(х - 2)) = (x - 2)( 2x + 5x-10) = (x-2)(7x:-10). | | у(2х + 5у) = (х- 2)(2x + 5(х - 2)) = (x - 2)( 2x + 5x-10) = (x-2)(7x:-10). |
| | | | |
| - | \В подобных случаях после приобретения некоторого опыта можно не вводить новую переменную, а использовать следующую
| + | В подобных случаях после приобретения некоторого опыта можно не вводить новую переменную, а использовать следующую |
| | | | |
| | 2х(х - 2) + 5(х - 2)<sup>2</sup> = (х - 2)(2x + 5(x - 2))= (х - 2)(2х + 5х~ 10) = (х - 2)(7x - 10). <br> <br> | | 2х(х - 2) + 5(х - 2)<sup>2</sup> = (х - 2)(2x + 5(x - 2))= (х - 2)(2х + 5х~ 10) = (х - 2)(7x - 10). <br> <br> |
| | | | |
| - | <br> <sub>Учебники по всему предметам [[Математика|скачать]], разработка планов уроков для учителей, Математика для 7 класса [[Гипермаркет знаний - первый в мире!|онлайн]]</sub>
| + | <sub>Календарно-тематичне планування з математики, [http://xvatit.com/it/audio_television/ '''відео'''] з математики [[Гіпермаркет Знань - перший в світі!|онлайн]], Математика в школі [[Математика|скачати]]</sub> |
| | | | |
| | <br> <br> | | <br> <br> |
| Строка 93: |
Строка 93: |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://http://school.xvatit.com/index.php?title=Категория:Вынесение_общего_множителя_за_скобки._Задачи_и_упражнения задачи и упражнения] | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=Категория:Вынесение_общего_множителя_за_скобки._Задачи_и_упражнения задачи и упражнения] |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
Текущая версия на 05:50, 15 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Вынесение общего множителя за скобки
Вынесение общего множителя за скобки
Прежде чем начинать изучение этого параграфа, вернитесь к § 15. Там мы уже рассмотрели пример, в котором требовалось представить многочлен в виде произведения многочлена и одночлена. Мы установили, что эта задача не всегда корректна. Если все же такое произведение удалось составить, то обычно говорят, вынесение что многочлен разложен на множители с помощью общего вынесения общего множителя за скобки. Рассмотрим несколько примеров.
Пример 1. Разложить на множители многочлен:
а) 2х + 6у, в) 4а3 + 6а2; д) 5а4 - 10а3 + 15а8.
б) а3 + а2; г) 12аЬ4 - 18а2b3с;
Р е ш е н и е.
а) 2х + 6у = 2 (x + Зу). За скобки вынесли общий делитель коэффициентов членов многочлена.
б) а3 + а2 = а2(а + 1). Если одна и та же переменная входит во все члены многочлена, то ее можно вынести за скобки в степени, равной наименьшей из имеющихся (т. е. выбирают наименьший из имеющихся показателей).
в) Здесь используем тот же прием, что и при решении примеров а) и б): для коэффициентов находим общий делитель (в данном случае число 2), для переменных — наименьшую степень из имеющихся (в данном случае а2). Получаем:
4а3 + 6а2 = 2а2 • 2а + 2а2 • 3 = 2а2 (2а + 3).
г) Обычно для целочисленных коэффициентов стараются найти не просто общий делитель, а наибольший общий делитель. Для коэффициентов 12 и 18 им будет число 6. Замечаем, что переменная а входит в оба члена многочлена, при этом наименьший показапоказатель равен 1. Переменная b также входит в оба члена многочлена, причем наименьший показатель равен 3. Наконец, переменная с входит только во второй член многочлена и не входит в первый член, значит, эту переменную нельзя вынести за скобки ни в какой степени. В итоге имеем:
12аb4 - 18а2Ь3с = 6аЬ3 • 2b - 6аЬ3 • Зас = 6аb3(2b - Зас).
д) 5а4-10а3+15а8 = 5а3(а-2 + За2).
Фактически в этом примере мы выработали следующий алгоритм.

Замечание. В ряде случаев полезно выносить за скобку в качестве общего множителя и дробный коэффициент.
Например:
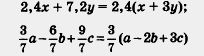
Пример 2. Разложить на множители:
-х4у3-2х3у2 + 5х2.
Решение. Воспользуемся сформулированным алгоритмом.
1) Наибольший общий делитель коэффициентов -1, -2 и 5 равен 1.
2) Переменная х входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки х2.
3) Переменная у входит не во все члены многочлена; значит, ее нельзя вынести за скобки.
В ы в о д: за скобки можно вынести х2. Правда, в данном случае целесообразнее вынести за скобки -x2.
Получим:
-х4у3 -2х3у2+ 5х2 = - х2(х2 у3 + 2ху2 - 5).
Пример 3. Можно ли разделить многочлен 5а4 - 10а3 + 15а5 на одночлен 5а3? Если да, то выполнить деление.
Решение. В примере 1д) мы получили, что
5а4 - 10а3 + 15а8 - 5а3(а - 2 + За2).
Значит, заданный многочлен можно разделить на 5а3, при этом в частном получится а - 2 + За2.
Подобные примеры мы рассматривали в § 18; просмотрите их, пожалуйста, еще раз, но уже с точки зрения вынесения общего множителя за скобки.
Разложение многочлена на множители с помощью вынесения общего множителя за скобки тесно связано с двумя операциями, которые мы изучали в § 15 и 18, — с умножением многочлена на одночлен и с делением многочлена на одночлен.
А теперь несколько расширим наши представления о вынесении общего множителя за скобки. Дело в том, что иногда алгебраическое выражение задается в таком виде, что в качестве общего множителя может выступать не одночлен, а сумма нескольких одночленов.
Пример 4. Разложить на множители:
2x(x-2) + 5(x-2)2.
Решение. Введем новую переменную у = х - 2. Тогда получим:
2x (x - 2) + 5 (x - 2)2 = 2ху + 5у2.
Замечаем, что переменную у можно вынести за скобки:
2ху + 5у2 — у (2х + 5у). А теперь вернемся к старым обозначениям:
у(2х + 5у) = (х- 2)(2x + 5(х - 2)) = (x - 2)( 2x + 5x-10) = (x-2)(7x:-10).
В подобных случаях после приобретения некоторого опыта можно не вводить новую переменную, а использовать следующую
2х(х - 2) + 5(х - 2)2 = (х - 2)(2x + 5(x - 2))= (х - 2)(2х + 5х~ 10) = (х - 2)(7x - 10).
Календарно-тематичне планування з математики, відео з математики онлайн, Математика в школі скачати
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|