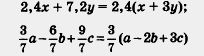|
|
| (8 промежуточных версий не показаны.) |
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Вынесение общего множителя за скобки</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Вынесение общего множителя за скобки, многочлен? степень, одночлен, алгебраическое выражение</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Вынесение общего множителя за скобки''' | + | <br> '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Вынесение общего множителя за скобки''' |
| | | | |
| - | <br> | + | <br> ''' '''[[Вынесение общего множителя за скобки. Задачи|'''Вынесение общего множителя за скобки''']]'''<br> ''' |
| | | | |
| - | <br>
| + | Прежде чем начинать изучение этого параграфа, вернитесь к § 15. Там мы уже рассмотрели пример, в котором требовалось представить '''[[Розклад многочленів на множники. Винесення спільного множника за дужки. Задачі та вправи|многочлен]]''' в виде произведения многочлена и одночлена. Мы установили, что эта задача не всегда корректна. Если все же такое произведение удалось составить, то обычно говорят, вынесение что многочлен разложен на множители с помощью общего вынесения общего множителя за скобки. Рассмотрим несколько примеров. |
| | | | |
| - | ''' ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ ''' | + | <br> '''Пример 1.''' Разложить на множители многочлен: |
| | | | |
| - | <br>Прежде чем начинать изучение этого параграфа, вернитесь к § 15. Там мы уже рассмотрели пример, в котором требоk валось представить многочлен в виде произведения многочлена и одночлена. Мы установили, что эта задача не всегда корректна. Если все же такое про? изведение удалось составить, то обычно говорят, вынесение что многочлен разложен на множители с помощью общего вынесения общего множителя за скобки. Рассмотрим несколько примеров. | + | <br> а) 2х + 6у, в) 4а<sup>3</sup> + 6а<sup>2</sup>; д) 5а<sup>4</sup> - 10а<sup>3</sup> + 15а<sup>8</sup>. <br>б) а<sup>3</sup> + а<sup>2</sup>; г) 12аЬ<sup>4</sup> - 18а<sup>2</sup>b<sup>3</sup>с;<br> <br>'''Р е ш е н и е.'''<br> а) 2х + 6у = 2 (x + Зу). За скобки вынесли общий делитель коэффициентов членов многочлена.<br> |
| | | | |
| - | '''Пример 1.''' Разложить на множители многочлен:
| + | б) а<sup>3</sup> + а<sup>2</sup> = а<sup>2</sup>(а + 1). Если одна и та же переменная входит во все члены многочлена, то ее можно вынести за скобки в степени, равной наименьшей из имеющихся (т. е. выбирают наименьший из имеющихся показателей).<br> |
| | | | |
| - | а) 2х + 6у, в) 4а<sup>3</sup> + 6а<sup>2</sup>; д) 5а<sup>4</sup> - 10а<sup>3</sup> + 15а<sup>8</sup>. <br>б) а<sup>3</sup> + а<sup>2</sup>; г) 12аЬ<sup>4</sup> - 18а<sup>2</sup>Ь<sup>3</sup>с; | + | в) Здесь используем тот же прием, что и при решении примеров а) и б): для коэффициентов находим общий делитель (в данном случае число 2), для переменных — наименьшую '''[[Свойства степени с натуральным показателем|степень]]''' из имеющихся (в данном случае а<sup>2</sup>). Получаем: <br> |
| | | | |
| - | <br>'''Р е ш е н и е.''' | + | 4а<sup>3</sup> + 6а<sup>2</sup> = 2а<sup>2</sup> • 2а + 2а<sup>2</sup> • 3 = 2а<sup>2</sup> (2а + 3).<br> |
| | | | |
| - | а) 2х + 6у = 2 (x + Зу). За скобки вынесли общий делитель коэффициентов членов многочлена.
| + | г) Обычно для целочисленных коэффициентов стараются найти не просто общий делитель, а наибольший общий делитель. Для коэффициентов 12 и 18 им будет число 6. Замечаем, что переменная а входит в оба члена многочлена, при этом наименьший показапоказатель равен 1. Переменная b также входит в оба члена многочлена, причем наименьший показатель равен 3. Наконец, переменная с входит только во второй член многочлена и не входит в первый член, значит, эту переменную нельзя вынести за скобки ни в какой степени. В итоге имеем:<br> |
| | | | |
| - | б) а<sup>3</sup> + а<sup>2</sup> = а<sup>2</sup>(а + 1). Если одна и та же переменная входит во все члены многочлена, то ее можно вынести за скобки в степени, равной наименьшей из имеющихся (т. е. выбирают наименьший из имеющихся показателей).
| + | 12аb<sup>4</sup> - 18а<sup>2</sup>Ь<sup>3</sup>с = 6аЬ<sup>3</sup> • 2b - 6аЬ<sup>3</sup> • Зас = 6аb<sup>3</sup>(2b - Зас).<br> |
| | | | |
| - | в) Здесь используем тот же прием, что и при решении примеров а) и б): для коэффициентов находим общий делитель (в данном случае число 2), для переменных — наименьшую степень из имеющихся (в данном случае а<sup>2</sup>). Получаем: 4а<sup>3</sup> + 6а<sup>2</sup> = 2а<sup>2</sup> • 2а + 2а<sup>2</sup> • 3 = 2а<sup>2</sup> (2а + 3).
| + | д) 5а<sup>4</sup>-10а<sup>3</sup>+15а<sup>8</sup> = 5а<sup>3</sup>(а-2 + За<sup>2</sup>).<br> |
| | | | |
| - | г) Обычно для целочисленных коэффициентов стараются найти не просто общий делитель, а наибольший общий делитель. Для коэффициентов 12 и 18 им будет число 6. Замечаем, что переменная а входит в оба члена многочлена, при этом наименьший показапоказатель равен 1. Переменная Ь также входит в оба члена многочлена, причем наименьший показатель равен 3. Наконец, переменная с входит только во второй член многочлена и не входит в первый <br>член, значит, эту переменную нельзя вынести за скобки ни в какой степени. В итоге имеем:
| + | Фактически в этом примере мы выработали следующий алгоритм. |
| | | | |
| - | 12аb<sup>4</sup> - 18а<sup>2</sup>Ь<sup>3</sup>с = 6аЬ<sup>3</sup> • 2b - 6аЬ<sup>3</sup> • Зас = 6аb<sup>3</sup>(2b - Зас).
| + | <br> [[Image:08-06-27.jpg|480px|Алгоритм]] |
| | | | |
| - | д) 5а<sup>4</sup>-10а<sup>3</sup>+15а<sup>8</sup> = 5а<sup>3</sup>(а-2 + За<sup>2</sup>).
| + | <br> '''''Замечание'''''. В ряде случаев полезно выносить за скобку в качестве общего множителя и дробный коэффициент. <br> |
| | | | |
| - | Фактически в этом примере мы выработали следующий алгоритм.
| + | Например: |
| | | | |
| - | [[Image:08-06-27.jpg]] | + | <br> [[Image:08-06-28.jpg|240px|Дробный коэффициент выносится за скобку]] |
| | | | |
| - | <br><br>'''''Замечание'''''. В ряде случаев полезно выносить за скобку в качестве общего множителя и дробный коэффициент. Например:
| + | <br> '''Пример 2.''' Разложить на множители: |
| | | | |
| - | [[Image:08-06-28.jpg]]
| + | -х<sup>4</sup>у<sup>3</sup>-2х<sup>3</sup>у<sup>2</sup> + 5х<sup>2</sup>. |
| | | | |
| - | '''Пример 2.''' Разложить на множители:
| + | Решение. Воспользуемся сформулированным алгоритмом. |
| | | | |
| - | -х<sup>4</sup>у<sup>3</sup>-2х<sup>3</sup>у<sup>2</sup> + 5х<sup>2</sup>. <br>Решение. Воспользуемся сформулированным алгоритмом.
| + | <br> 1) Наибольший общий делитель коэффициентов -1, -2 и 5 равен 1. <br>2) Переменная х входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки х<sup>2</sup>. <br>3) Переменная у входит не во все члены многочлена; значит, ее нельзя вынести за скобки. |
| | | | |
| - | 1) Наибольший общий делитель коэффициентов -1, -2 и 5 равен 1. <br>2) Переменная х входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки х<sup>2</sup>. <br>3) Переменная у входит не во все члены многочлена; значит, ее нельзя вынести за скобки.
| + | '''В ы в о д:''' за скобки можно вынести х<sup>2</sup>. Правда, в данном случае целесообразнее вынести за скобки -x<sup>2</sup>. |
| | | | |
| - | '''В ы в о д:''' за скобки можно вынести х<sup>2</sup>. Правда, в данном случае целесообразнее вынести за скобки -x<sup>2</sup>.
| + | Получим: <br>-х<sup>4</sup>у<sup>3</sup> -2х<sup>3</sup>у<sup>2</sup>+ 5х<sup>2 </sup>= - х<sup>2</sup>(х<sup>2</sup> у<sup>3</sup> + 2ху<sup>2</sup> - 5). |
| | | | |
| - | Получим: <br>-х<sup>4</sup>у<sup>3</sup> -2х<sup>3</sup>у<sup>2</sup>+ 5х<sup>2 </sup>= - х<sup>2</sup>(х<sup>2</sup> у<sup>3</sup> + 2ху<sup>2</sup> - 5).
| + | '''Пример 3'''. Можно ли разделить многочлен 5а<sup>4</sup> - 10а<sup>3</sup> + 15а<sup>5</sup> на одночлен 5а<sup>3</sup>? Если да, то выполнить '''[[Умножение и деление степеней с одинаковыми показателями|деление]]'''. |
| - | | + | |
| - | '''Пример 3'''. Можно ли разделить многочлен 5а<sup>4</sup> - 10а<sup>3</sup> + 15а<sup>5</sup> на одночлен 5а<sup>3</sup>? Если да, то выполнить деление. | + | |
| | | | |
| | Решение. В примере 1д) мы получили, что | | Решение. В примере 1д) мы получили, что |
| | | | |
| - | 5а<sup>4 </sup>- 10а<sup>3</sup> + 15а<sup>8</sup> - 5а<sup>3</sup>(а - 2 + За<sup>2</sup>). <br>Значит, заданный многочлен можно разделить на 5а<sup>3</sup>, при этом в частном получится а - 2 + За<sup>2</sup>. <br>Подобные примеры мы рассматривали в § 18; просмотрите их, пожалуйста, еще раз, но уже с точки зрения вынесения общего множителя за скобки. <br> Разложение многочлена на множители с помо щью вынесения общего множителя за скобки тесно связано с двумя операциями, которые мы изучали <br>в § 15 и 18, — с умножением многочлена на одночлен и с делением многочлена на одночлен. | + | 5а<sup>4 </sup>- 10а<sup>3</sup> + 15а<sup>8</sup> - 5а<sup>3</sup>(а - 2 + За<sup>2</sup>). |
| | | | |
| - | А теперь несколько расширим наши представления о вынесении общего множителя за скобки. Дело в том, что иногда алгебраическое выражение задается в таком виде, что в качестве общего множителя может выступать не одночлен, а сумма нескольких одночленов. | + | Значит, заданный многочлен можно разделить на 5а<sup>3</sup>, при этом в частном получится а - 2 + За<sup>2</sup>. |
| | + | |
| | + | Подобные примеры мы рассматривали в § 18; просмотрите их, пожалуйста, еще раз, но уже с точки зрения вынесения общего множителя за скобки. |
| | + | |
| | + | Разложение многочлена на множители с помощью вынесения общего множителя за скобки тесно связано с двумя операциями, которые мы изучали в § 15 и 18, — с умножением многочлена на одночлен и с делением многочлена на '''[[Одночлен. Піднесення одночленів до степеня. Множення одночленів|одночлен]]'''. |
| | + | |
| | + | А теперь несколько расширим наши представления о вынесении общего множителя за скобки. Дело в том, что иногда '''[[Основное свойство алгебраической дроби|алгебраическое выражение]]''' задается в таком виде, что в качестве общего множителя может выступать не одночлен, а сумма нескольких одночленов. |
| | | | |
| | '''Пример 4.''' Разложить на множители: | | '''Пример 4.''' Разложить на множители: |
| Строка 59: |
Строка 63: |
| | 2x(x-2) + 5(x-2)<sup>2</sup>. | | 2x(x-2) + 5(x-2)<sup>2</sup>. |
| | | | |
| - | Решение. Введем новую переменную у = х - 2. Тогда получим: <br>2x (x - 2) + 5 (x - 2)<sup>2</sup> = 2ху + 5у<sup>2</sup>. | + | Решение. Введем новую переменную у = х - 2. Тогда получим: |
| | + | |
| | + | 2x (x - 2) + 5 (x - 2)<sup>2</sup> = 2ху + 5у<sup>2</sup>. |
| | | | |
| | Замечаем, что переменную у можно вынести за скобки: | | Замечаем, что переменную у можно вынести за скобки: |
| Строка 65: |
Строка 71: |
| | 2ху + 5у<sup>2</sup> — у (2х + 5у). А теперь вернемся к старым обозначениям: | | 2ху + 5у<sup>2</sup> — у (2х + 5у). А теперь вернемся к старым обозначениям: |
| | | | |
| - | у(2х + 5у) = (х- 2)(2x + 5(х - 2)) = (x - 2)( 2x + 5x-10) = (x-2)(7x:-10). | + | у(2х + 5у) = (х- 2)(2x + 5(х - 2)) = (x - 2)( 2x + 5x-10) = (x-2)(7x:-10). |
| | | | |
| | В подобных случаях после приобретения некоторого опыта можно не вводить новую переменную, а использовать следующую | | В подобных случаях после приобретения некоторого опыта можно не вводить новую переменную, а использовать следующую |
| | | | |
| - | 2х(х - 2) + 5(х - 2)<sup>2</sup> = (х - 2)(2x + 5(x - 2))= (х - 2)(2х + 5х~ 10) = (х - 2)(7x - 10). <br><br><br><br> | + | 2х(х - 2) + 5(х - 2)<sup>2</sup> = (х - 2)(2x + 5(x - 2))= (х - 2)(2х + 5х~ 10) = (х - 2)(7x - 10). <br> <br> |
| | | | |
| - | <br> | + | <sub>Календарно-тематичне планування з математики, [http://xvatit.com/it/audio_television/ '''відео'''] з математики [[Гіпермаркет Знань - перший в світі!|онлайн]], Математика в школі [[Математика|скачати]]</sub> |
| | | | |
| - | <br> | + | <br> <br> |
| | | | |
| - | <sub>Учебники по всему предметам [[Математика|скачать]], разработка планов уроков для учителей, Математика для 7 класса [[Гипермаркет знаний - первый в мире!|онлайн]]</sub>
| + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=Категория:Вынесение_общего_множителя_за_скобки._Задачи_и_упражнения задачи и упражнения] |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| - | '''<u></u>''' | + | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
| Строка 129: |
Строка 135: |
| | <br> | | <br> |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам]. | + | <br> Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам]. |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум]. | + | <br> Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум]. |
Прежде чем начинать изучение этого параграфа, вернитесь к § 15. Там мы уже рассмотрели пример, в котором требовалось представить многочлен в виде произведения многочлена и одночлена. Мы установили, что эта задача не всегда корректна. Если все же такое произведение удалось составить, то обычно говорят, вынесение что многочлен разложен на множители с помощью общего вынесения общего множителя за скобки. Рассмотрим несколько примеров.
в) Здесь используем тот же прием, что и при решении примеров а) и б): для коэффициентов находим общий делитель (в данном случае число 2), для переменных — наименьшую степень из имеющихся (в данном случае а2). Получаем:
г) Обычно для целочисленных коэффициентов стараются найти не просто общий делитель, а наибольший общий делитель. Для коэффициентов 12 и 18 им будет число 6. Замечаем, что переменная а входит в оба члена многочлена, при этом наименьший показапоказатель равен 1. Переменная b также входит в оба члена многочлена, причем наименьший показатель равен 3. Наконец, переменная с входит только во второй член многочлена и не входит в первый член, значит, эту переменную нельзя вынести за скобки ни в какой степени. В итоге имеем:
Фактически в этом примере мы выработали следующий алгоритм.
Решение. Воспользуемся сформулированным алгоритмом.
Решение. В примере 1д) мы получили, что
Подобные примеры мы рассматривали в § 18; просмотрите их, пожалуйста, еще раз, но уже с точки зрения вынесения общего множителя за скобки.
Разложение многочлена на множители с помощью вынесения общего множителя за скобки тесно связано с двумя операциями, которые мы изучали в § 15 и 18, — с умножением многочлена на одночлен и с делением многочлена на одночлен.
А теперь несколько расширим наши представления о вынесении общего множителя за скобки. Дело в том, что иногда алгебраическое выражение задается в таком виде, что в качестве общего множителя может выступать не одночлен, а сумма нескольких одночленов.
Решение. Введем новую переменную у = х - 2. Тогда получим:
В подобных случаях после приобретения некоторого опыта можно не вводить новую переменную, а использовать следующую