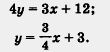|
|
|
| (3 промежуточные версии не показаны) | | Строка 1: |
Строка 1: |
| - | <metakejavascript:void(0)ywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Основные понятия</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Основные понятия, линейное уравнение, математический язык, математическая модель, уравнения, графики, системы</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Основные понятия''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Основные понятия''' |
| Строка 7: |
Строка 7: |
| | <br> | | <br> |
| | | | |
| - | '''ОСНОВНЫЕ ПОНЯТИЯ ''' | + | '''Основные понятия''' |
| | | | |
| - | <br>В § 28 мы ввели понятие линейного уравнения с двумя переменными — так называют равенство ax + by + с = 0, где а, Ь, с — конкретные числа, причем [[Image:09-06-78.jpg]] — переменные (неизвестные). <br>Примеры линейных уравнений с двумя переменными: <br>2х - bу + 1 = 0; <br>х + у - 3 = 0; <br>s - 5t + 4 = 0 <br>(здесь переменные обозначены по-другому: s, t, — но это роли не играет). | + | <br>В § 28 мы ввели понятие линейного уравнения с двумя переменными — так называют равенство ax + by + с = 0, где а, b, с — конкретные числа, причем [[Image:09-06-78.jpg|120px|Переменные]] — переменные (неизвестные). <br>Примеры линейных уравнений с двумя переменными: <br>2х - bу + 1 = 0; <br>х + у - 3 = 0; <br>s - 5t + 4 = 0 <br>(здесь переменные обозначены по-другому: s, t, — но это роли не играет). |
| | | | |
| - | В том же § 28 мы ввели понятие решения линейного уравнения с двумя переменными — так называют всякую пару чисел (х; у), которая удовлетворяет уравнению, т. е. обращает равенство с переменными ax + by + с = 0 в верное числовое равенство. На первом месте всегда пишут значение переменной х, на втором — значение переменной у. | + | В том же § 28 мы ввели понятие решения '''[[Линейное уравнение с двумя переменными и его график|линейного уравнения]]''' с двумя переменными — так называют всякую пару чисел (х; у), которая удовлетворяет уравнению, т. е. обращает равенство с переменными ax + by + с = 0 в верное числовое равенство. На первом месте всегда пишут значение переменной х, на втором — значение переменной у. |
| | | | |
| - | Приведем примеры: <br>1. (2; 3) — решение уравнения 5x + Зу - 19 = 0. В самом деле, 5 • 2 + 3 • 3 - 19 = 0 — верное числовое равенство. <br>2. (-4; 2) — решение уравнения Зх - у + 14 = 0. Действительно, 3 • (-4) -2 + 14 = 0 — верное числовое равенство. <br>3.[[Image:09-06-79.jpg]] — решение уравнения - 0,4а: + Зу + 7 = 0. Имеем: | + | Приведем примеры: <br>1. (2; 3) — решение уравнения 5x + Зу - 19 = 0. В самом деле, 5 • 2 + 3 • 3 - 19 = 0 — верное числовое равенство. <br>2. (-4; 2) — решение уравнения Зх - у + 14 = 0. Действительно, 3 • (-4) -2 + 14 = 0 — верное числовое равенство. <br>3.[[Image:09-06-79.jpg|60px|Решение уравнения]] — решение уравнения - 0,4а: + Зу + 7 = 0. Имеем: |
| | | | |
| - | [[Image:09-06-80.jpg]] — верное числовое равенство. <br>4. (1; 2) не является решением уравнения 2х - Зу + 1 = 0. В самом деле, 2 •1-3 •2 + 1 = 0 — неверное числовое равенство (получается, что -3 = 0). <br>В § 29 мы отмечали, что математическую модель ах + by + + с = 0 всегда можно заменить более простой: у = kx + m. Например, уравнение Зх - 4у + 12 = 0 можно преобразовать так: | + | [[Image:09-06-80.jpg|180px|Верное числовое равенство]] — верное числовое равенство. <br>4. (1; 2) не является решением уравнения 2х - Зу + 1 = 0. В самом деле, 2 •1-3 •2 + 1 = 0 — неверное числовое равенство (получается, что -3 = 0). <br>В § 29 мы отмечали, что '''[[Что такое математическая модель|математическую модель]]''' ах + by + + с = 0 всегда можно заменить более простой: у = kx + m. Например, уравнение Зх - 4у + 12 = 0 можно преобразовать так: |
| | | | |
| - | [[Image:09-06-81.jpg]]<br>Графиком линейного уравнения ах + by + с = 0 является прямая (см. § 28). Координаты любой точки этой прямой удовлетворяют уравнению ах + by + с = 0, т. е. являются решением уравнения. Сколько же решений имеет уравнение ах + by + с = 0? Столько же, сколько точек расположено на прямой, служащей графиком уравнения ах + by + с = 0, т. е. бесконечное множество решений. | + | [[Image:09-06-81.jpg|120px|Преобразование уравнения]]<br>Графиком линейного уравнения ах + by + с = 0 является прямая (см. § 28). Координаты любой точки этой прямой удовлетворяют уравнению ах + by + с = 0, т. е. являются решением уравнения. Сколько же решений имеет уравнение ах + by + с = 0? Столько же, сколько точек расположено на прямой, служащей графиком уравнения ах + by + с = 0, т. е. бесконечное множество решений. |
| | | | |
| - | Многие реальные ситуации при переводе на математический язык оформляются в виде математической модели, состоящей из двух линейных уравнений с двумя переменными. С такой ситуацией мы встретились в § 28 в задаче про двух садоводов Иванова и Петрова: | + | Многие реальные ситуации при переводе на '''[[Что такое математический язык|математический язык]]''' оформляются в виде математической модели, состоящей из двух линейных уравнений с двумя переменными. С такой ситуацией мы встретились в § 28 в задаче про двух садоводов Иванова и Петрова: |
| | | | |
| | математическая модель состояла из двух уравнений: <br>5x - 2у = 0 и 3x + 2у - 16 = 0, причем нас интересовала такая пара значений (х; у), которая одновременно удовлетворяла и тому, и другому уравнению. В таких случаях обычно не говорят, что математическая модель состоит из двух уравнений, а говорят, что математическая модель представляет собой систему уравнений. | | математическая модель состояла из двух уравнений: <br>5x - 2у = 0 и 3x + 2у - 16 = 0, причем нас интересовала такая пара значений (х; у), которая одновременно удовлетворяла и тому, и другому уравнению. В таких случаях обычно не говорят, что математическая модель состоит из двух уравнений, а говорят, что математическая модель представляет собой систему уравнений. |
| Строка 25: |
Строка 25: |
| | Вообще, если даны два линейных уравнения с двумя переменными х и у: a<sub>1</sub>x + b<sub>1</sub>y + c<sub>1</sub> = 0 и а<sub>2</sub>х + b<sub>2</sub>y + с<sub>2</sub> = 0 и поставлена задача — найти такие пары значений (х; у), которые одновременно удовлетворяют и тому, и другому уравнению, то говорят, что заданные уравнения образуют систему уравнений. | | Вообще, если даны два линейных уравнения с двумя переменными х и у: a<sub>1</sub>x + b<sub>1</sub>y + c<sub>1</sub> = 0 и а<sub>2</sub>х + b<sub>2</sub>y + с<sub>2</sub> = 0 и поставлена задача — найти такие пары значений (х; у), которые одновременно удовлетворяют и тому, и другому уравнению, то говорят, что заданные уравнения образуют систему уравнений. |
| | | | |
| - | равнения <br>системы записывают друг под другом и объединяют специальным символом — фигурной скобкой: <br>[[Image:09-06-82.jpg]]<br>Пару значений (х; у), которая одновременно является решением и первого, и второго уравнений системы, называют решением системы. <br>Решить систему — это значит найти все ее решения или установить, что их нет. <br>Теперь мы можем сказать, что уже встречались с системой линейных уравнений — математическая модель уже упомянутой задачи про садоводов из § 28 выглядела так:
| + | Уравнения системы записывают друг под другом и объединяют специальным символом — фигурной скобкой: |
| | | | |
| - | [[Image:09-06-83.jpg]]<br><br>Ее решением была пара (2; 5), т. е. х = 2, у = 5. <br>Рассмотрим новые примеры. <br>'''Пример 1.''' Решить систему уравнений | + | <br>[[Image:09-06-82.jpg|360px|Уравнения системы]] |
| | | | |
| - | [[Image:09-06-84.jpg]]<br><br>Решение. Графиком уравнения х + 2у - 5 = 0 является прямая. Найдем две пары значений переменных х, у, удовлетворяющих этому уравнению. Если у = 0, то из уравнения х + 2у - 5 = 0 находим: х = 5. Если х = 0, то из уравнения х + 2у - 5 = 0 находим: у = 2,5. Итак, нашли две точки: (5; 0) и (0; 2,5). Построим на <br>координатной плоскости хОу прямую, проходящую через эти две точки, — прямая l<sub>1</sub> на рисунке 70.
| + | <br>Пару значений (х; у), которая одновременно является решением и первого, и второго уравнений '''[[Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций|системы]]''', называют решением системы. |
| | | | |
| - | Графиком уравнения 2х + \у + 3 = 0 также является прямая.
| + | Решить систему — это значит найти все ее решения или установить, что их нет. |
| | | | |
| - | Найдем две пары значений переменных х, у, удовлетворяющих этому уравнению. Если у = 0, то из уравнения 2х + ±у + 3 = 0 находим: х = -1,5. Если х — 2,5, то из уравнения 2х + 4у + 3 = 0 находим: 5 + 4у + 3 = 0, и, следовательно, у = -2. Итак, нашли две точки: (-1,5; 0) и (2,5; -2). Построим на координатной плоскости хОу прямую, проходящую через эти две точки, — прямая I<sub>2</sub> на рисунке 70. | + | Теперь мы можем сказать, что уже встречались с системой линейных уравнений — математическая модель уже упомянутой задачи про садоводов из § 28 выглядела так: |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:09-06-83.jpg|360px|Математическая модель]]<br><br>Ее решением была пара (2; 5), т. е. х = 2, у = 5. <br>Рассмотрим новые примеры. <br>'''Пример 1.''' Решить систему уравнений |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:09-06-84.jpg|360px|Математическая модель]]<br><br>Решение. Графиком уравнения х + 2у - 5 = 0 является прямая. Найдем две пары значений переменных х, у, удовлетворяющих этому уравнению. Если у = 0, то из уравнения х + 2у - 5 = 0 находим: х = 5. Если х = 0, то из уравнения х + 2у - 5 = 0 находим: у = 2,5. Итак, нашли две точки: (5; 0) и (0; 2,5). Построим на <br>координатной плоскости хОу прямую, проходящую через эти две точки, — прямая l<sub>1</sub> на рисунке 70. |
| | + | |
| | + | Графиком уравнения 2х + у + 3 = 0 также является прямая. |
| | + | |
| | + | Найдем две пары значений переменных х, у, удовлетворяющих этому уравнению. Если у = 0, то из '''[[Линейное уравнение с двумя переменными и его график|уравнения]]''' 2х + ±у + 3 = 0 находим: х = -1,5. Если х — 2,5, то из уравнения 2х + 4у + 3 = 0 находим: 5 + 4у + 3 = 0, и, следовательно, у = -2. Итак, нашли две точки: (-1,5; 0) и (2,5; -2). Построим на координатной плоскости хОу прямую, проходящую через эти две точки, — прямая I<sub>2</sub> на рисунке 70. |
| | | | |
| | Прямые l<sub>1</sub> и I<sub>2</sub> параллельны. Что означает этот геометрический факт для данной системы уравнений? То, что она не имеет решений (поскольку нет точек, удовлетворяющих одновременно и тому, и другому уравнению, т.е. принадлежащих одновременно и той, и другой из построенных прямых I<sub>1</sub> и I<sub>2</sub>). | | Прямые l<sub>1</sub> и I<sub>2</sub> параллельны. Что означает этот геометрический факт для данной системы уравнений? То, что она не имеет решений (поскольку нет точек, удовлетворяющих одновременно и тому, и другому уравнению, т.е. принадлежащих одновременно и той, и другой из построенных прямых I<sub>1</sub> и I<sub>2</sub>). |
| Строка 41: |
Строка 53: |
| | '''Пример 2.''' Найти два числа, если известно, что их сумма равна 39, а разность равна 11. <br>Решение. Если х, у — искомые числа, то х + у = 39 и x - y = 11, причем эти равенства должны одновременно выполняться: | | '''Пример 2.''' Найти два числа, если известно, что их сумма равна 39, а разность равна 11. <br>Решение. Если х, у — искомые числа, то х + у = 39 и x - y = 11, причем эти равенства должны одновременно выполняться: |
| | | | |
| - | [[Image:09-06-85.jpg]] | + | [[Image:09-06-85.jpg|360px|Математическая модель]] |
| | | | |
| | <br>Получили систему двух линейных уравнений с двумя переменными. | | <br>Получили систему двух линейных уравнений с двумя переменными. |
| Строка 47: |
Строка 59: |
| | Можно угадать, чему равны х и у: х = 25, у = 14. Но, во-первых, метод угадывания далеко не всегда применим на практике. А во-вторых, где гарантия, что иного решения нет, может быть, мы просто до него не додумались, не «доугадали». | | Можно угадать, чему равны х и у: х = 25, у = 14. Но, во-первых, метод угадывания далеко не всегда применим на практике. А во-вторых, где гарантия, что иного решения нет, может быть, мы просто до него не додумались, не «доугадали». |
| | | | |
| - | Можно построить графики уравнений х + у = 39 и х - у = 11, это прямые, причем непараллельные (в отличие от тех, что в примере 1), они пересекаются в одной точке. Эту точку мы уже знаем: (25; 14); значит, это единственная пара чисел, которая нас устраивает, единственное решение системы. <br>Ответ: 25 и 14. | + | Можно построить '''[[Приклади графіків залежностей між величинами|графики]]''' уравнений х + у = 39 и х - у = 11, это прямые, причем непараллельные (в отличие от тех, что в примере 1), они пересекаются в одной точке. Эту точку мы уже знаем: (25; 14); значит, это единственная пара чисел, которая нас устраивает, единственное решение системы. |
| | | | |
| - | [[Image:09-06-86.jpg]]<br><br>В примерах 1 и 2 мы применили графический метод решения системы линейных уравнений. Этим же методом мы пользовались в § 28 при решении задачи о числе яблонь у двух садоводов (система B) решена в § 28 графическим методом). | + | Ответ: 25 и 14. |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:09-06-86.jpg|480px|Графический метод решения системы линейных уравнений]]<br><br>В примерах 1 и 2 мы применили графический метод решения системы линейных уравнений. Этим же методом мы пользовались в § 28 при решении задачи о числе яблонь у двух садоводов (система B) решена в § 28 графическим методом). |
| | | | |
| | К сожалению, графический метод, как и метод угадывания, не самый надежный. Во-первых, прямые могут просто не уместиться на чертеже. Во- вторых, прямые могут уместиться на чертеже, но пересечься в точке, координаты которой по чертежу не очень легко определить. | | К сожалению, графический метод, как и метод угадывания, не самый надежный. Во-первых, прямые могут просто не уместиться на чертеже. Во- вторых, прямые могут уместиться на чертеже, но пересечься в точке, координаты которой по чертежу не очень легко определить. |
| Строка 55: |
Строка 71: |
| | '''Пример 3'''. Решить систему уравнений: | | '''Пример 3'''. Решить систему уравнений: |
| | | | |
| - | [[Image:09-06-87.jpg]]<br><br>Решение. Построим графики уравнений системы. Сначала, как это чаще всего мы делаем, преобразуем оба уравнения к виду линейной функции. Из первого уравнения получаем: у = 3x - 5, а из второго: у = 7 - 2х. | + | [[Image:09-06-87.jpg|360px|Математическая модель]]<br><br>Решение. Построим графики уравнений системы. Сначала, как это чаще всего мы делаем, преобразуем оба уравнения к виду линейной функции. Из первого уравнения получаем: у = 3x - 5, а из второго: у = 7 - 2х. |
| | | | |
| - | Построим в одной системе координат графики линейных функций у = Зx - 5 (прямая l<sub>1</sub> на рис. 71) и у — 7 - 2х (прямая 12 на рис. 71). Они пересекаются в точке А, координаты которой — единственное решение заданной системы. А вот чему конкретно равны абсцисса и ордината точки A, мы по рисунку 71 точно определить не сможем (постройте эти прямые в своих тетрадях в клеточку и убедитесь, что точка А как бы «висит» внутри определенной клеточки). Придется <br>нам позднее вернуться к этому примеру. | + | Построим в одной системе координат графики линейных функций у = Зx - 5 (прямая l<sub>1</sub> на рис. 71) и у — 7 - 2х (прямая 12 на рис. 71). Они пересекаются в точке А, координаты которой — единственное решение заданной системы. А вот чему конкретно равны абсцисса и ордината точки A, мы по рисунку 71 точно определить не сможем (постройте эти прямые в своих тетрадях в клеточку и убедитесь, что точка А как бы «висит» внутри определенной клеточки). Придется нам позднее вернуться к этому примеру. |
| | | | |
| - | [[Image:09-06-88.jpg]]
| + | <br> |
| | | | |
| - | Но все-таки графический метод решения системы линейных уравнений имеет большое значение. С его помощью можно сделать следующие важные выводы'. <br>графиками обоих уравнений системы (1) являются прямые; эти прямые могут пересекаться, причем только в одной точке, — это значит, что система (1) имеет единственное решение (так было в рассмотренных в этом параграфе системах (2), (4), (5); эти прямые могут быть параллельны — это значит, что система не имеет решений (говорят также, что система несовместна — такой была система (3)); эти прямые могут совпасть — это значит, что система имеет бесконечно много решений (говорят также, что система неопределенна).
| + | [[Image:09-06-88.jpg|180px|График линейной функции]] |
| | | | |
| - | Итак, мы познакомились с новой математической моделью (1) — системой двух линейных уравнений с двумя переменными. Наша задача — научиться ее решать. Метод угадывания ненадежен, графический метод также выручает не всегда. Значит, нам нужно располагать надежными алгебраическими методами решения системы двух линейных уравнений с двумя переменными. Об этом и пойдет речь в следующих параграфах. <br><br><br><br> | + | <br> |
| | + | |
| | + | Но все-таки графический метод решения системы линейных уравнений имеет большое значение. С его помощью можно сделать следующие важные выводы, графиками обоих уравнений системы (1) являются прямые; эти прямые могут пересекаться, причем только в одной точке, — это значит, что система (1) имеет единственное решение (так было в рассмотренных в этом параграфе системах (2), (4), (5); эти прямые могут быть параллельны — это значит, что система не имеет решений (говорят также, что система несовместна — такой была система (3)); эти прямые могут совпасть — это значит, что система имеет бесконечно много решений (говорят также, что система неопределенна). |
| | + | |
| | + | Итак, мы познакомились с новой '''[[Что такое математическая модель|математической моделью]]''' (1) — системой двух линейных уравнений с двумя переменными. Наша задача — научиться ее решать. Метод угадывания ненадежен, графический метод также выручает не всегда. Значит, нам нужно располагать надежными алгебраическими методами решения системы двух линейных уравнений с двумя переменными. Об этом и пойдет речь в следующих параграфах. <br><br><br> |
| | + | |
| | + | <br> <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| | + | |
| | + | <br> |
| | | | |
| - | <sub>Математика для 7 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> <br>
| + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 15:59, 15 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Основные понятия
Основные понятия
В § 28 мы ввели понятие линейного уравнения с двумя переменными — так называют равенство ax + by + с = 0, где а, b, с — конкретные числа, причем 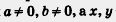 — переменные (неизвестные). — переменные (неизвестные).
Примеры линейных уравнений с двумя переменными:
2х - bу + 1 = 0;
х + у - 3 = 0;
s - 5t + 4 = 0
(здесь переменные обозначены по-другому: s, t, — но это роли не играет).
В том же § 28 мы ввели понятие решения линейного уравнения с двумя переменными — так называют всякую пару чисел (х; у), которая удовлетворяет уравнению, т. е. обращает равенство с переменными ax + by + с = 0 в верное числовое равенство. На первом месте всегда пишут значение переменной х, на втором — значение переменной у.
Приведем примеры:
1. (2; 3) — решение уравнения 5x + Зу - 19 = 0. В самом деле, 5 • 2 + 3 • 3 - 19 = 0 — верное числовое равенство.
2. (-4; 2) — решение уравнения Зх - у + 14 = 0. Действительно, 3 • (-4) -2 + 14 = 0 — верное числовое равенство.
3.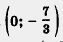 — решение уравнения - 0,4а: + Зу + 7 = 0. Имеем: — решение уравнения - 0,4а: + Зу + 7 = 0. Имеем:
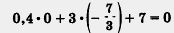 — верное числовое равенство. — верное числовое равенство.
4. (1; 2) не является решением уравнения 2х - Зу + 1 = 0. В самом деле, 2 •1-3 •2 + 1 = 0 — неверное числовое равенство (получается, что -3 = 0).
В § 29 мы отмечали, что математическую модель ах + by + + с = 0 всегда можно заменить более простой: у = kx + m. Например, уравнение Зх - 4у + 12 = 0 можно преобразовать так:
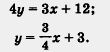
Графиком линейного уравнения ах + by + с = 0 является прямая (см. § 28). Координаты любой точки этой прямой удовлетворяют уравнению ах + by + с = 0, т. е. являются решением уравнения. Сколько же решений имеет уравнение ах + by + с = 0? Столько же, сколько точек расположено на прямой, служащей графиком уравнения ах + by + с = 0, т. е. бесконечное множество решений.
Многие реальные ситуации при переводе на математический язык оформляются в виде математической модели, состоящей из двух линейных уравнений с двумя переменными. С такой ситуацией мы встретились в § 28 в задаче про двух садоводов Иванова и Петрова:
математическая модель состояла из двух уравнений:
5x - 2у = 0 и 3x + 2у - 16 = 0, причем нас интересовала такая пара значений (х; у), которая одновременно удовлетворяла и тому, и другому уравнению. В таких случаях обычно не говорят, что математическая модель состоит из двух уравнений, а говорят, что математическая модель представляет собой систему уравнений.
Вообще, если даны два линейных уравнения с двумя переменными х и у: a1x + b1y + c1 = 0 и а2х + b2y + с2 = 0 и поставлена задача — найти такие пары значений (х; у), которые одновременно удовлетворяют и тому, и другому уравнению, то говорят, что заданные уравнения образуют систему уравнений.
Уравнения системы записывают друг под другом и объединяют специальным символом — фигурной скобкой:

Пару значений (х; у), которая одновременно является решением и первого, и второго уравнений системы, называют решением системы.
Решить систему — это значит найти все ее решения или установить, что их нет.
Теперь мы можем сказать, что уже встречались с системой линейных уравнений — математическая модель уже упомянутой задачи про садоводов из § 28 выглядела так:

Ее решением была пара (2; 5), т. е. х = 2, у = 5.
Рассмотрим новые примеры.
Пример 1. Решить систему уравнений

Решение. Графиком уравнения х + 2у - 5 = 0 является прямая. Найдем две пары значений переменных х, у, удовлетворяющих этому уравнению. Если у = 0, то из уравнения х + 2у - 5 = 0 находим: х = 5. Если х = 0, то из уравнения х + 2у - 5 = 0 находим: у = 2,5. Итак, нашли две точки: (5; 0) и (0; 2,5). Построим на
координатной плоскости хОу прямую, проходящую через эти две точки, — прямая l1 на рисунке 70.
Графиком уравнения 2х + у + 3 = 0 также является прямая.
Найдем две пары значений переменных х, у, удовлетворяющих этому уравнению. Если у = 0, то из уравнения 2х + ±у + 3 = 0 находим: х = -1,5. Если х — 2,5, то из уравнения 2х + 4у + 3 = 0 находим: 5 + 4у + 3 = 0, и, следовательно, у = -2. Итак, нашли две точки: (-1,5; 0) и (2,5; -2). Построим на координатной плоскости хОу прямую, проходящую через эти две точки, — прямая I2 на рисунке 70.
Прямые l1 и I2 параллельны. Что означает этот геометрический факт для данной системы уравнений? То, что она не имеет решений (поскольку нет точек, удовлетворяющих одновременно и тому, и другому уравнению, т.е. принадлежащих одновременно и той, и другой из построенных прямых I1 и I2).
Ответ: система не имеет решений.
Пример 2. Найти два числа, если известно, что их сумма равна 39, а разность равна 11.
Решение. Если х, у — искомые числа, то х + у = 39 и x - y = 11, причем эти равенства должны одновременно выполняться:

Получили систему двух линейных уравнений с двумя переменными.
Можно угадать, чему равны х и у: х = 25, у = 14. Но, во-первых, метод угадывания далеко не всегда применим на практике. А во-вторых, где гарантия, что иного решения нет, может быть, мы просто до него не додумались, не «доугадали».
Можно построить графики уравнений х + у = 39 и х - у = 11, это прямые, причем непараллельные (в отличие от тех, что в примере 1), они пересекаются в одной точке. Эту точку мы уже знаем: (25; 14); значит, это единственная пара чисел, которая нас устраивает, единственное решение системы.
Ответ: 25 и 14.
В примерах 1 и 2 мы применили графический метод решения системы линейных уравнений. Этим же методом мы пользовались в § 28 при решении задачи о числе яблонь у двух садоводов (система B) решена в § 28 графическим методом).
К сожалению, графический метод, как и метод угадывания, не самый надежный. Во-первых, прямые могут просто не уместиться на чертеже. Во- вторых, прямые могут уместиться на чертеже, но пересечься в точке, координаты которой по чертежу не очень легко определить.
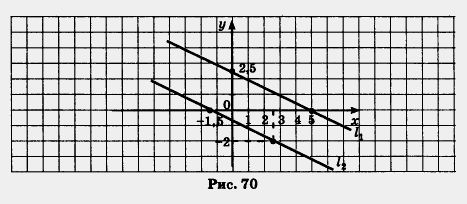
Пример 3. Решить систему уравнений:

Решение. Построим графики уравнений системы. Сначала, как это чаще всего мы делаем, преобразуем оба уравнения к виду линейной функции. Из первого уравнения получаем: у = 3x - 5, а из второго: у = 7 - 2х.
Построим в одной системе координат графики линейных функций у = Зx - 5 (прямая l1 на рис. 71) и у — 7 - 2х (прямая 12 на рис. 71). Они пересекаются в точке А, координаты которой — единственное решение заданной системы. А вот чему конкретно равны абсцисса и ордината точки A, мы по рисунку 71 точно определить не сможем (постройте эти прямые в своих тетрадях в клеточку и убедитесь, что точка А как бы «висит» внутри определенной клеточки). Придется нам позднее вернуться к этому примеру.
Но все-таки графический метод решения системы линейных уравнений имеет большое значение. С его помощью можно сделать следующие важные выводы, графиками обоих уравнений системы (1) являются прямые; эти прямые могут пересекаться, причем только в одной точке, — это значит, что система (1) имеет единственное решение (так было в рассмотренных в этом параграфе системах (2), (4), (5); эти прямые могут быть параллельны — это значит, что система не имеет решений (говорят также, что система несовместна — такой была система (3)); эти прямые могут совпасть — это значит, что система имеет бесконечно много решений (говорят также, что система неопределенна).
Итак, мы познакомились с новой математической моделью (1) — системой двух линейных уравнений с двумя переменными. Наша задача — научиться ее решать. Метод угадывания ненадежен, графический метод также выручает не всегда. Значит, нам нужно располагать надежными алгебраическими методами решения системы двух линейных уравнений с двумя переменными. Об этом и пойдет речь в следующих параграфах.
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|