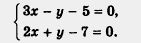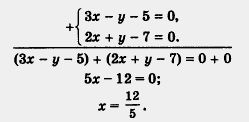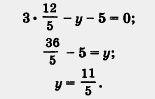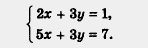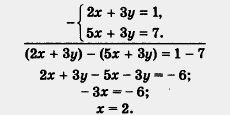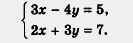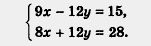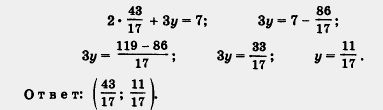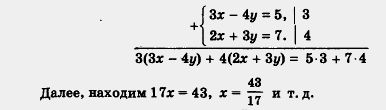|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Метод алгебраического сложения</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Метод алгебраического сложения, системы, уравнение, переменная, множители</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Метод алгебраического сложения''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Метод алгебраического сложения''' |
| Строка 9: |
Строка 9: |
| | ''' Метод алгебраического сложения''' | | ''' Метод алгебраического сложения''' |
| | | | |
| - | <br>Мы довольно часто возвращаемся к тому, что уже обсудили ранее, например для того, чтобы рассмотреть ситуацию под другим углом зрения. Вот и теперь давайте вернемся к примеру 1 из § 36, где речь шла о решении системы уравнений | + | <br>Мы довольно часто возвращаемся к тому, что уже обсудили ранее, например для того, чтобы рассмотреть ситуацию под другим углом зрения. Вот и теперь давайте вернемся к примеру 1 из § 36, где речь шла о решении '''[[Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций|системы]]''' уравнений |
| | | | |
| | <br> | | <br> |
| Строка 15: |
Строка 15: |
| | [[Image:09-06-98.jpg|180px|Математическая модель]]<br><br>Как мы решали эту систему? Мы выразили у из первого уравнения и подставили результат во второе, что привело к уравнению с одной переменной х, т.е. фактически к временному исключению из рассмотрения переменной у. Но исключить у из рассмотрения можно было бы значительно проще — достаточно сложить оба уравнения системы (сложить уравнения — это значит по отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять): | | [[Image:09-06-98.jpg|180px|Математическая модель]]<br><br>Как мы решали эту систему? Мы выразили у из первого уравнения и подставили результат во второе, что привело к уравнению с одной переменной х, т.е. фактически к временному исключению из рассмотрения переменной у. Но исключить у из рассмотрения можно было бы значительно проще — достаточно сложить оба уравнения системы (сложить уравнения — это значит по отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять): |
| | | | |
| - | [[Image:09-06-99.jpg|240px|Метод алгебраического сложения]]<br><br>Затем можно было найденное значение х подставить в любое уравнение системы, например в первое, и найти у: | + | [[Image:09-06-99.jpg|240px|Метод алгебраического сложения]]<br><br>Затем можно было найденное значение х подставить в любое '''[[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнение]]''' системы, например в первое, и найти у: |
| | | | |
| | [[Image:09-06-100.jpg|240px|Метод алгебраического сложения]] | | [[Image:09-06-100.jpg|240px|Метод алгебраического сложения]] |
| Строка 35: |
Строка 35: |
| | '''Пример 2.''' Решить систему уравнений: | | '''Пример 2.''' Решить систему уравнений: |
| | | | |
| - | [[Image:09-06-103.jpg|180px|Математическая модель]]<br><br>Решение. Здесь сразу исключить переменную х или переменную у из обоих уравнений с помощью сложения или вычитания уравнений не удастся. Нужен подготовительный этап. Сначала умножим все члены первого уравнения системы на 3, а все члены второго уравнения — на 4. Получим: | + | [[Image:09-06-103.jpg|180px|Математическая модель]]<br><br>Решение. Здесь сразу исключить '''[[Линейное уравнение с двумя переменными и его график|переменную]]''' х или переменную у из обоих уравнений с помощью сложения или вычитания уравнений не удастся. Нужен подготовительный этап. Сначала умножим все члены первого уравнения системы на 3, а все члены второго уравнения — на 4. Получим: |
| | | | |
| | [[Image:09-06-104.jpg|180px|Математическая модель]]<br><br>Теперь можно сложить уравнения, что приведет к исключению переменной у. | | [[Image:09-06-104.jpg|180px|Математическая модель]]<br><br>Теперь можно сложить уравнения, что приведет к исключению переменной у. |
| Строка 45: |
Строка 45: |
| | [[Image:09-06-106.jpg|480px|Метод алгебраического сложения]]<br><br><br>Можно использовать следующую краткую запись приведенного решения: | | [[Image:09-06-106.jpg|480px|Метод алгебраического сложения]]<br><br><br>Можно использовать следующую краткую запись приведенного решения: |
| | | | |
| - | [[Image:09-06-107.jpg|480px|Метод алгебраического сложения]]<br><br>Здесь справа от вертикальной черты записаны дополнительные множители, с помощью которых удалось уравнять коэффициенты при переменной у в обоих уравнениях системы. <br>Метод, который мы обсудили в этом параграфе, называют методом алгебраического сложения<br> | + | [[Image:09-06-107.jpg|480px|Метод алгебраического сложения]]<br><br>Здесь справа от вертикальной черты записаны дополнительные '''[[Розклад многочленів на множники. Винесення спільного множника за дужки. Задачі та вправи|множители]]''', с помощью которых удалось уравнять коэффициенты при переменной у в обоих уравнениях системы. <br>Метод, который мы обсудили в этом параграфе, называют методом алгебраического сложения<br> |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <sub>Помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], Математика для 7 класса [[Математика|скачать]], календарно-тематическое планирование</sub> <br> | + | <br> <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| | | | |
| | <br> | | <br> |
Текущая версия на 16:21, 15 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Метод алгебраического сложения
Метод алгебраического сложения
Мы довольно часто возвращаемся к тому, что уже обсудили ранее, например для того, чтобы рассмотреть ситуацию под другим углом зрения. Вот и теперь давайте вернемся к примеру 1 из § 36, где речь шла о решении системы уравнений
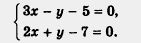
Как мы решали эту систему? Мы выразили у из первого уравнения и подставили результат во второе, что привело к уравнению с одной переменной х, т.е. фактически к временному исключению из рассмотрения переменной у. Но исключить у из рассмотрения можно было бы значительно проще — достаточно сложить оба уравнения системы (сложить уравнения — это значит по отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять):
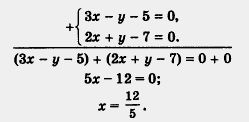
Затем можно было найденное значение х подставить в любое уравнение системы, например в первое, и найти у:
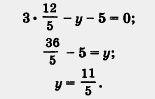
Попробуем применить аналогичные рассуждения еще для нескольких систем линейных уравнений с двумя переменными.
Пример 1. Решить систему уравнений:
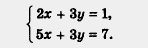
Р е ш е н и е. 1) Вычтем второе уравнение из первого:
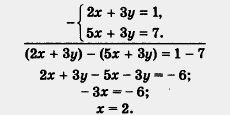
2) Подставим найденное значение х = 2 в первое уравнение заданной системы, т. е. в уравнение 2х + 3y - 1:
2 . 2 + 3y= 1;
3y = - 4
y = - 1
3) Пара х = 2, у = -1— решение заданной системы.
Ответ:2;-1).
Пример 2. Решить систему уравнений:
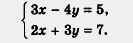
Решение. Здесь сразу исключить переменную х или переменную у из обоих уравнений с помощью сложения или вычитания уравнений не удастся. Нужен подготовительный этап. Сначала умножим все члены первого уравнения системы на 3, а все члены второго уравнения — на 4. Получим:
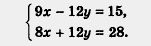
Теперь можно сложить уравнения, что приведет к исключению переменной у.
Имеем: 17х = 43, т. е.
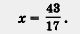
Подставим найденное значение х во второе уравнение исходной системы, т.е. в уравнение 2х +3y = 7:
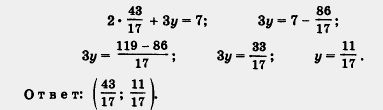
Можно использовать следующую краткую запись приведенного решения:
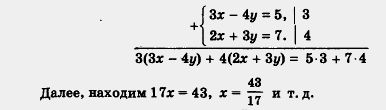
Здесь справа от вертикальной черты записаны дополнительные множители, с помощью которых удалось уравнять коэффициенты при переменной у в обоих уравнениях системы.
Метод, который мы обсудили в этом параграфе, называют методом алгебраического сложения
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|