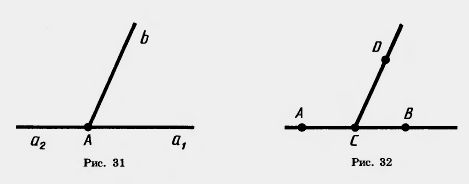|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Смежные углы</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Смежные углы, полупрямая, точка, угол, теорема</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Смежные углы''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Смежные углы''' |
| Строка 17: |
Строка 17: |
| | Из теоремы 2.1 следует, что если '''''два угла равны, то смежные с ними углы равны.''''' | | Из теоремы 2.1 следует, что если '''''два угла равны, то смежные с ними углы равны.''''' |
| | | | |
| - | Из теоремы 2.1 следует также, что '''''если '''[[Практикум на тему «Суміжні кути, їх властивості»|'''Угол''''''не развернутый, то его градусная мера меньше 180°.''''' | + | Из теоремы 2.1 следует также, что если '''[[Практикум на тему «Суміжні кути, їх властивості»|угол]]''' не развернутый, то его градусная мера меньше 180°. |
| | | | |
| | Задача (3). Найдите смежные углы, если один из них в два раза больше другого. | | Задача (3). Найдите смежные углы, если один из них в два раза больше другого. |
| Строка 39: |
Строка 39: |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | [http://xvatit.com/relax/fun-videos/ '''<sub>Видео</sub>''']<sub>по математике [[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | + | [http://xvatit.com/relax/fun-videos/ '''<sub>Видео</sub>''']<sub>по математике [[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| | | | |
| | <br> | | <br> |
Текущая версия на 15:22, 17 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Смежные углы
Смежные углы
Определение. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (а1b) и (a2b) смежные. У них сторона b общая, а стороны a1 и а2 являются дополнительными полупрямыми.
Пусть С — точка на прямой АВ, лежащая между точками А и В, а D — точка, не лежащая на прямой АВ (рис. 32). Тогда углы BCD и ACD смежные. У них сторона CD общая. Стороны СА и СВ являются дополнительными полупрямыми прямой АВ, так как точки А и В этих полупрямых разделяются начальной точкой С.
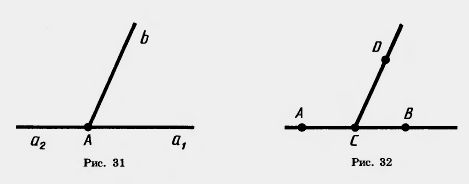
Теорема 2.1. Сумма смежных углов равна 180°.
Доказательство. Пусть  (a1b) и (a1b) и  (а2b) — данные смежные углы (см. рис. 31). Луч b проходит между сторонами а1 и а2 развернутого угла. Поэтому сумма углов (а1b) и (a2b) равна развернутому углу, т. е. 180°. Теорема доказана. (а2b) — данные смежные углы (см. рис. 31). Луч b проходит между сторонами а1 и а2 развернутого угла. Поэтому сумма углов (а1b) и (a2b) равна развернутому углу, т. е. 180°. Теорема доказана.
Из теоремы 2.1 следует, что если два угла равны, то смежные с ними углы равны.
Из теоремы 2.1 следует также, что если угол не развернутый, то его градусная мера меньше 180°.
Задача (3). Найдите смежные углы, если один из них в два раза больше другого.
Решение. Обозначим градусную меру меньшего из углов через х. Тогда градусная мера большего угла будет 2х. Сумма углов равна 180°. Итак,
x + 2x = 180, 3x = 180.
Отсюда x = 60. Значит, наши смежные углы равны 60° и 120°.
Угол, равный 90°, называется прямым углом.
Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол.
Угол, меньший 90°, называется острым углом. Угол, больший 90° и меньший 180°, называется тупым.
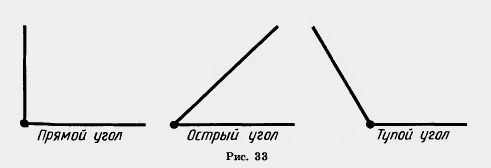
Так как сумма смежных углов равна 180°, то угол, смежный с острым углом, тупой, а угол, смежный с тупым углом, острый. На рисунке 33 изображены три вида углов.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Видеопо математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|