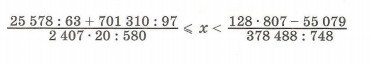|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 4 класс, урок, на Тему, Урок 14, Координаты на плоскости </metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 4 класс, урок, на Тему, Урок 14, Координаты на плоскости, точка, угол</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 4 класс|Математика 4 класс]]>> Урок 14. Координаты на плоскости ''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 4 класс|Математика 4 класс]]>> Урок 14. Координаты на плоскости ''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | <br> | + | [[Image:4.02-48.jpg|640px|Урок 14. Координаты на плоскости]]<br> '''<br>'''1. Используя принцип координат, рассмотренный на предыдущих уроках, придумай разумный способ обозначения точек прямого угла парами чисел.<br><br>[[Image:4.02-49.jpg|640px|Координаты на плоскости]] |
| | | | |
| - | [[Image:4.02-48.jpg]]<br> '''<br><br>1. Используя принцип координат, рассмотренный на предыдущих уроках, придумай разумный способ обозначения точек прямого угла парами чисел.'''<br><br>[[Image:4.02-49.jpg]] | + | На предыдущих уроках мы познакомились с практическим использованием принципа координат. Подобным образом обозначается и положение '''[[Урок 15. Построение точек по их координатам|точек]]''' на плоскости. Для этого строят прямой угол, стороны которого являются координатными лучами с общим началом в вершине угла (рис. 1). Такой угол называют координатным углом. <br>[[Image:4.02-50.jpg|240px|Координаты на плоскости]]<br><br>Одну из сторон координатного угла располагают горизонтально и называют осью абсцисс Ох, а другую сторону — вертикально и называют осью ординат Оси координат Ох и Оу выделяют на чертеже стрелками. Чтобы обозначить числами положение любой точки координатного '''[[Урок 2. Развернутый угол. Смежные углы|угла]]''' , надо провести перпендикулярные прямые к сторонам угла и назвать сначала абсциссу (координату на оси Ох), а затем ординату (координату на оси Оу). Так, например, точка А имеет абсциссу 2 и ординату 5, значит, координатами точки А является пара чисел (2; 5). Пишут: А (2; 5). При определении '''[[Координатная прямая|координат]]''' точки нельзя путать их порядок. Например, если поменять местами абсциссу и ординату точки А, то получится другая точка В (5; 2), которая показана на рис. 1.<br> <br>'''''Внимание!!!''''' Запись А (2; 5) можно прочитать разными способами:<br><br>— Точка А с абсциссой 2 и ординатой 5.<br>— Точка А с координатами 2 и 5.<br>— Координаты точки А — пара чисел 2 и 5.<br><br>'''2. Найди верные записи и прочитай их различными способами. Неверные записи зачеркни и исправь ошибки.'''<br> <br>[[Image:4.02-51.jpg|640px|Задачи]]<br><br>'''3. Запиши координаты точек, обозначенных на рисунке:'''<br> <br>[[Image:4.02-52.jpg|640px|Координатная плоскость]]<br>'''<br>4. Найди координаты вершин многоугольников:'''<br>[[Image:4.02-53.jpg|640px|Координатная плоскость]]<br>'''<br>5. Расшифруй высказывание великого немецкого математика Карла Гаусса (1777— 1855).'''<br><br>[[Image:4.02-54.jpg|640px|Задачи]]<br> <br>6*. Рассказывают, что, когда Карл Гаусс учился в начальной школе, его [http://xvatit.com/vuzi/ '''учитель,'''] чтобы занять класс на продолжительное время самостоятельной работой, дал детям трудное задание — вычислить сумму всех натуральных чисел от 1 до 100. Но маленький Гаусс это задание выполнил почти моментально. Попробуй и ты быстро выполнить это задание.<br>''' <br>7*. Как быстро вычислить:'''<br><br>а) 1 + 3 + 5 + ... + 995 + 997 + 999; |
| | | | |
| - | На предыдущих уроках мы познакомились с практическим использованием принципа координат. Подобным образом обозначается и положение точек на плоскости. Для этого строят прямой угол, стороны которого являются координатными лучами с общим началом в вершине угла (рис. 1). Такой угол называют координатным углом.<br> <br>[[Image:4.02-50.jpg]]<br><br>Одну из сторон координатного угла располагают горизонтально и называют осью абсцисс Ох, а другую сторону — вертикально и называют осью ординат Оси координат Ох и Оу выделяют на чертиже стрелками. Чтобы обозначить числами положение любой точки координатного угла, надо провести перпендикулярные прямые к сторонам угла и назвать сначала абсциссу (координату на оси Ох), а затем ординату (координату на оси Оу). Так, например, точка А имеет абсциссу 2 и ординату 5, значит, координатами точки А является пара чисел (2; 5). Пишут: А (2; 5). При определении координат точки нельзя путать их порядок. Например, если поменять местами абсциссу и ординату точки А, то получится другая точка В (5; 2), которая показана на рис. 1.<br> <br>'''''Внимание!!!'''''Запись А (2; 5) можно прочитать разными способами:<br><br>— Точка А с абсциссой 2 и ординатой 5.<br>— Точка А с координатами 2 и 5.<br>— Координаты точки А — пара чисел 2 и 5.
| + | б) 99 - 97 + 95 - 93 + 91 - 89 + ... + 7 - 5 + 3 - 1?<br> <br>8. Какие знаки арифметических действий надо поставить вместо звездочек в записи [[Image:4.02-55.jpg|Задача]], чтобы получить 8? Чтобы получить 20? 5<br> <br>9. Рассмотри схемы. В каких случаях произойдет встреча? Найди скорость сближения или скорость удаления и вычисли расстояние между объектами через 3 ч после начала движения.<br> <br>[[Image:4.02-56.jpg|640px|Задачи]]<br>'''<br>'''10. Два грузовика выехали одновременно навстречу друг другу из двух городов, расстояние между которыми равно 360 км. Скорость одного грузовика 36 км/ч, что составляет [[Image:28.01-116.jpg]] скорости второго грузовика. Через сколько времени они встретятся?'''<br>'''<br>11. Патрульный катер заметил шхуну контрабандистов, когда она находилась на расстоянии 1 км 600 м от него. Сколько времени потребуется катеру, чтобы догнать шхуну, если он движется со скоростью 500 м/мин, а скорость шхуны составляет лишь 92% скорости катера. Успеет ли шхуна доплыть до нейтральных вод, если ее отделяют от них 20 км 700 м?'''<br><br>12. Вычисли значения выражений:'''<br><br>а) 5000 - (3612 : х + 47) : 18 при х = 84; |
| - | | + | |
| - | <br><br>'''2. Найди верные записи и прочитай их различными способами. Неверные записи зачеркни и исправь ошибки.'''<br> <br>[[Image:4.02-51.jpg]]<br><br>'''3. Запиши координаты точек, обозначенных на рисунке:'''<br> <br>[[Image:4.02-52.jpg]]<br>'''<br>4. Найди координаты вершин многоугольников:'''<br>[[Image:4.02-53.jpg]]<br>'''<br>5. Расшифруй высказывание великого немецкого математика Карла Гаусса (1777— 1855).'''<br><br>[[Image:4.02-54.jpg]]<br> <br>'''6*. Рассказывают, что, когда Карл Гаусс учился в начальной школе, его учитель, чтобы занять класс на продолжительное время самостоятельной работой, дал детям трудное задание — вычислить сумму всех натуральных чисел от 1 до 100. Но маленький Гаусс это задание выполнил почти моментально. Попробуй и ты быстро выполнить это задание.'''<br>''' <br>7*. Как быстро вычислить:'''<br><br>а) 1 + 3 + 5 + ... + 995 + 997 + 999;
| + | |
| - | | + | |
| - | б) 99 - 97 + 95 - 93 + 91 - 89 + ... + 7 - 5 + 3 - 1?<br> <br>'''8. Какие знаки арифметических действий надо поставить вместо звездочек в записи [[Image:4.02-55.jpg]], чтобы получить 8? Чтобы получить 20? 5<br> <br>9. Рассмотри схемы. В каких случаях произойдет встреча? Найди скорость сближения или скорость удаления и вычисли расстояние между объектами через 3 ч после начала движения.'''<br> <br>[[Image:4.02-56.jpg]]<br>'''<br>10. Два грузовика выехали одновременно навстречу друг другу из двух городов, расстояние между которыми равно 360 км. Скорость одного грузовика 36 км/ч, что составляет [[Image:28.01-116.jpg]] скорости второго грузовика. Через сколько времени они встретятся?<br><br>11. Патрульный катер заметил шхуну контрабандистов, когда она находилась на расстоянии 1 км 600 м от него. Сколько времени потребуется катеру, чтобы догнать шхуну, если он движется со скоростью 500 м/мин, а скорость шхуны составляет лишь 92% скорости катера. Успеет ли шхуна доплыть до нейтральных вод, если ее отделяют от них 20 км 700 м?<br><br>12. Вычисли значения выражений:'''<br><br>а) 5000 - (3612 : х + 47) : 18 при х = 84; | + | |
| - | | + | |
| - | б) 998 + у : (79 • 97 + 1337) при у = 36 000.<br> <br>'''13. Запиши множество натуральных решений неравенства 7 < х [[Image:26.01-14.jpg]] 9. Является ли решением этого неравенства число [[Image:4.02-57.jpg]]?<br><br>14. Найди множество натуральных решений неравенства. Приведи несколько решений этого неравенства, не являющихся натуральными числами.'''<br> <br>[[Image:4.02-58.jpg]]
| + | |
| - | | + | |
| - | <br>
| + | |
| | | | |
| - | <br><br> | + | б) 998 + у : (79 • 97 + 1337) при у = 36 000.<br> <br>13. Запиши множество натуральных решений неравенства 7 < х [[Image:26.01-14.jpg]] 9. Является ли решением этого неравенства число [[Image:4.02-57.jpg]]?<br><br>14. Найди множество натуральных решений неравенства. Приведи несколько решений этого неравенства, не являющихся натуральными числами.<br> <br>[[Image:4.02-58.jpg|480px|Задачи]] |
| | | | |
| | <br> ''Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 3. - М.: Издательство "Ювента", 2005, - 64 с.: ил.'' | | <br> ''Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 3. - М.: Издательство "Ювента", 2005, - 64 с.: ил.'' |
Текущая версия на 12:00, 22 июля 2012
Гипермаркет знаний>>Математика>>Математика 4 класс>> Урок 14. Координаты на плоскости

1. Используя принцип координат, рассмотренный на предыдущих уроках, придумай разумный способ обозначения точек прямого угла парами чисел.
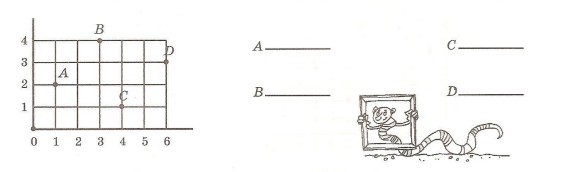
На предыдущих уроках мы познакомились с практическим использованием принципа координат. Подобным образом обозначается и положение точек на плоскости. Для этого строят прямой угол, стороны которого являются координатными лучами с общим началом в вершине угла (рис. 1). Такой угол называют координатным углом.
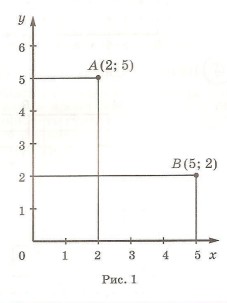
Одну из сторон координатного угла располагают горизонтально и называют осью абсцисс Ох, а другую сторону — вертикально и называют осью ординат Оси координат Ох и Оу выделяют на чертеже стрелками. Чтобы обозначить числами положение любой точки координатного угла , надо провести перпендикулярные прямые к сторонам угла и назвать сначала абсциссу (координату на оси Ох), а затем ординату (координату на оси Оу). Так, например, точка А имеет абсциссу 2 и ординату 5, значит, координатами точки А является пара чисел (2; 5). Пишут: А (2; 5). При определении координат точки нельзя путать их порядок. Например, если поменять местами абсциссу и ординату точки А, то получится другая точка В (5; 2), которая показана на рис. 1.
Внимание!!! Запись А (2; 5) можно прочитать разными способами:
— Точка А с абсциссой 2 и ординатой 5.
— Точка А с координатами 2 и 5.
— Координаты точки А — пара чисел 2 и 5.
2. Найди верные записи и прочитай их различными способами. Неверные записи зачеркни и исправь ошибки.
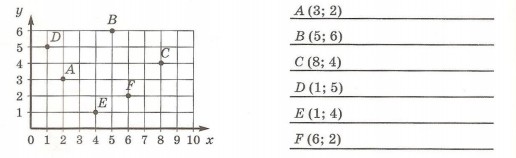
3. Запиши координаты точек, обозначенных на рисунке:
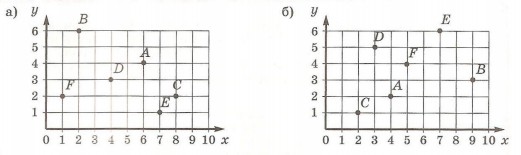
4. Найди координаты вершин многоугольников:
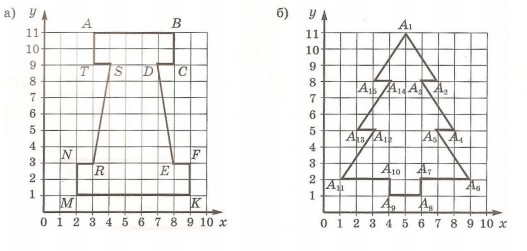
5. Расшифруй высказывание великого немецкого математика Карла Гаусса (1777— 1855).
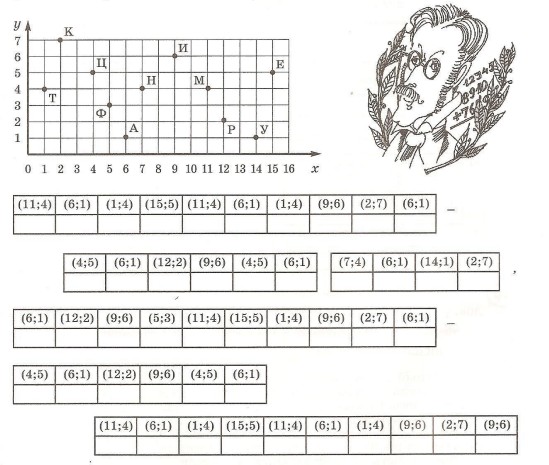
6*. Рассказывают, что, когда Карл Гаусс учился в начальной школе, его учитель, чтобы занять класс на продолжительное время самостоятельной работой, дал детям трудное задание — вычислить сумму всех натуральных чисел от 1 до 100. Но маленький Гаусс это задание выполнил почти моментально. Попробуй и ты быстро выполнить это задание.
7*. Как быстро вычислить:
а) 1 + 3 + 5 + ... + 995 + 997 + 999;
б) 99 - 97 + 95 - 93 + 91 - 89 + ... + 7 - 5 + 3 - 1?
8. Какие знаки арифметических действий надо поставить вместо звездочек в записи 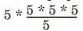 , чтобы получить 8? Чтобы получить 20? 5 , чтобы получить 8? Чтобы получить 20? 5
9. Рассмотри схемы. В каких случаях произойдет встреча? Найди скорость сближения или скорость удаления и вычисли расстояние между объектами через 3 ч после начала движения.
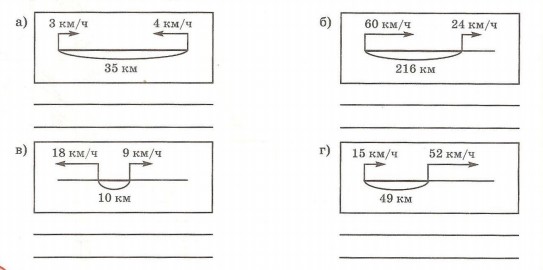
10. Два грузовика выехали одновременно навстречу друг другу из двух городов, расстояние между которыми равно 360 км. Скорость одного грузовика 36 км/ч, что составляет 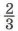 скорости второго грузовика. Через сколько времени они встретятся? скорости второго грузовика. Через сколько времени они встретятся?
11. Патрульный катер заметил шхуну контрабандистов, когда она находилась на расстоянии 1 км 600 м от него. Сколько времени потребуется катеру, чтобы догнать шхуну, если он движется со скоростью 500 м/мин, а скорость шхуны составляет лишь 92% скорости катера. Успеет ли шхуна доплыть до нейтральных вод, если ее отделяют от них 20 км 700 м?
12. Вычисли значения выражений:
а) 5000 - (3612 : х + 47) : 18 при х = 84;
б) 998 + у : (79 • 97 + 1337) при у = 36 000.
13. Запиши множество натуральных решений неравенства 7 < х 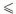 9. Является ли решением этого неравенства число 9. Является ли решением этого неравенства число 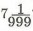 ? ?
14. Найди множество натуральных решений неравенства. Приведи несколько решений этого неравенства, не являющихся натуральными числами.
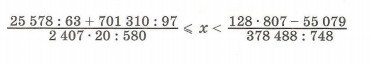
Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 3. - М.: Издательство "Ювента", 2005, - 64 с.: ил.
Помощь школьнику онлайн, Математика для 4 класса скачать, календарно-тематическое планирование
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|