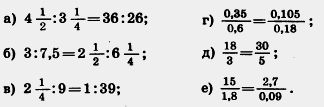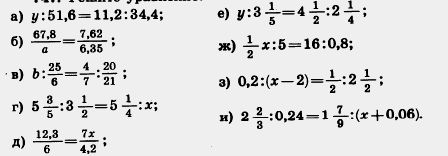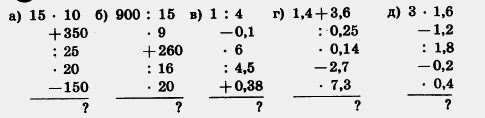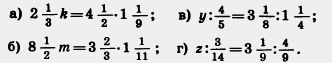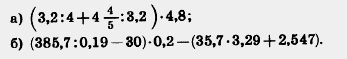|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 6 класс, Алгебра, урок, на Тему, Пропорции</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 6 класс, Алгебра, урок, на Тему, Пропорции, Отношения, пропорции, свойство пропорции, десятичной дроби, уравнение, число, процент попаданий</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Пропорции''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Пропорции''' |
| Строка 7: |
Строка 7: |
| | '''21. Пропорции''' | | '''21. Пропорции''' |
| | | | |
| - | <br>Отношения 3,6:1,2 и 6,3:2,1 равны, так как значения частных равны 3. Поэтому можно записать равенство 3,6:1,2 = 6,3:2,1, или [[Image:21-07-88.jpg|равенство]]<br>'''''Равенство двух отношений называют пропорцией.''''' | + | <br>'''[[Відношення. Основна властивість відношення.|Отношения]]''' 3,6:1,2 и 6,3:2,1 равны, так как значения частных равны 3. Поэтому можно записать равенство 3,6:1,2 = 6,3:2,1, или [[Image:21-07-88.jpg|равенство]]<br>'''''Равенство двух отношений называют пропорцией.''''' |
| | | | |
| | С помощью букв пропорцию записывают так: a:b = c:d или [[Image:21-07-89.jpg]] | | С помощью букв пропорцию записывают так: a:b = c:d или [[Image:21-07-89.jpg]] |
| Строка 13: |
Строка 13: |
| | Эти записи читают так: «Отношение а к b равно отношению с к d'''>>''' или «а так относится к b, как с относится к d'''>>'''.<br>В пропорции [[Image:21-07-89.jpg]], или a:b=c:d, <br> | | Эти записи читают так: «Отношение а к b равно отношению с к d'''>>''' или «а так относится к b, как с относится к d'''>>'''.<br>В пропорции [[Image:21-07-89.jpg]], или a:b=c:d, <br> |
| | | | |
| - | [[Image:21-07-90.jpg|120px|Пропорции]]<br>Числа a и d называют крайними членами, a числа b и с — средними членами пропорции. В дальнейшем будем считать, что все члены пропорции отличны от нуля: [[Image:21-07-91.jpg|Пропорции]].<br>В пропорции [[Image:21-07-88.jpg|Пропорции]] найдем произведение ее крайних и произведение ее средних членов. <br> | + | [[Image:21-07-90.jpg|120px|Пропорции]]<br>Числа a и d называют крайними членами, a числа b и с — средними членами '''[[Фішки для допитливих до уроку на тему «Пропорція»|пропорции]]'''. В дальнейшем будем считать, что все члены пропорции отличны от нуля: [[Image:21-07-91.jpg|Пропорции]].<br>В пропорции [[Image:21-07-88.jpg|Пропорции]] найдем произведение ее крайних и произведение ее средних членов. <br> |
| | | | |
| | Получим 3,6 • 2,1 = 7,56; 1,2 • 6,3 = 7,56. Значит, 3,6 • 2,1 = 1,2 • 6,3.<br> | | Получим 3,6 • 2,1 = 7,56; 1,2 • 6,3 = 7,56. Значит, 3,6 • 2,1 = 1,2 • 6,3.<br> |
| Строка 27: |
Строка 27: |
| | '''''Если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны.'''''<br> | | '''''Если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны.'''''<br> |
| | | | |
| - | Используя основное свойство пропорции, можно найти ее неизвестный член, если все остальные члены известны.<br> | + | Используя основное '''[[Пряма пропорційна залежність|свойство пропорции]]''', можно найти ее неизвестный член, если все остальные члены известны.<br> |
| | | | |
| | <u>Пример 1.</u> Найдем в пропорции 0,5: а = 2:13 неизвестный средний член а. <br> | | <u>Пример 1.</u> Найдем в пропорции 0,5: а = 2:13 неизвестный средний член а. <br> |
| Строка 33: |
Строка 33: |
| | Решение. Используя основное свойство пропорции, получим а • 2 = 0,5 • 13. Отсюда [[Image:21-07-92.jpg|Пропорции]]<br><br>Пример 2. Решим уравнение [[Image:21-07-93.jpg|Задание]] | | Решение. Используя основное свойство пропорции, получим а • 2 = 0,5 • 13. Отсюда [[Image:21-07-92.jpg|Пропорции]]<br><br>Пример 2. Решим уравнение [[Image:21-07-93.jpg|Задание]] |
| | | | |
| - | Решение. Используя основное свойство пропорции, получим [[Image:21-07-94.jpg|420px|Задание]] в виде десятичной дроби 3,75 и сократим выражение на 0,75, 8 75<br>имеем [[Image:21-07-95.jpg]] ; х= 1,75. | + | Решение. Используя основное свойство пропорции, получим [[Image:21-07-94.jpg|420px|Задание]] в виде '''[[Задачі до уроку «Порівняння десяткових дробів.»|десятичной дроби]]''' 3,75 и сократим выражение на 0,75, 8 75<br>имеем [[Image:21-07-95.jpg]] ; х= 1,75. |
| | | | |
| | ''' ?''' Что такое пропорция? Как называются числа х и у в пропорции х:а = b:у? Как называются числа x и y в пропорции x:y = a:b? Сформулируйте основное свойство пропорции. Какие перестановки членов пропорции снова приводят к верным пропорциям? Останется ли пропорция верной, если поменять местами какой-нибудь средний ее член с одним из крайних? Приведите пример. Останется ли пропорция верной, если оба средних члена поменять местами с крайними членами? Проверьте ваш ответ на пропорции 3:4 = 9:12. | | ''' ?''' Что такое пропорция? Как называются числа х и у в пропорции х:а = b:у? Как называются числа x и y в пропорции x:y = a:b? Сформулируйте основное свойство пропорции. Какие перестановки членов пропорции снова приводят к верным пропорциям? Останется ли пропорция верной, если поменять местами какой-нибудь средний ее член с одним из крайних? Приведите пример. Останется ли пропорция верной, если оба средних члена поменять местами с крайними членами? Проверьте ваш ответ на пропорции 3:4 = 9:12. |
| Строка 47: |
Строка 47: |
| | [[Image:21-07-100.jpg|320px|Задание]] | | [[Image:21-07-100.jpg|320px|Задание]] |
| | | | |
| - | 747. Решите уравнение: | + | 747. Решите '''[[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнение]]''': |
| | | | |
| | [[Image:21-07-101.jpg|480px|Задание]] | | [[Image:21-07-101.jpg|480px|Задание]] |
| Строка 61: |
Строка 61: |
| | [[Image:21-07-104.jpg|480px|Задание]]<br><br>752. Найдите отношение величин: | | [[Image:21-07-104.jpg|480px|Задание]]<br><br>752. Найдите отношение величин: |
| | | | |
| - | а) 1,5 м и 30 см;<br>б) 1 кг и 250 г;<br>в) 1 ч и 15 мин;<br>г) 50 см<sup>2</sup> и 1 дм<sup>2</sup>.<br><br>753. [[Image:21-07-105.jpg]] числа равны [[Image:21-07-106.jpg]] этого числа. Какое это число? | + | а) 1,5 м и 30 см;<br>б) 1 кг и 250 г;<br>в) 1 ч и 15 мин;<br>г) 50 см<sup>2</sup> и 1 дм<sup>2</sup>.<br><br>753. [[Image:21-07-105.jpg]] числа равны [[Image:21-07-106.jpg]] этого числа. Какое это '''[[Додавання і віднімання натуральних чисел|число]]'''? |
| | | | |
| | 754. Какое число надо прибавить к числителю и знаменателю дроби [[Image:21-07-107.jpg]], чтобы получить дробь [[Image:21-07-108.jpg]] ? | | 754. Какое число надо прибавить к числителю и знаменателю дроби [[Image:21-07-107.jpg]], чтобы получить дробь [[Image:21-07-108.jpg]] ? |
| Строка 69: |
Строка 69: |
| | а) четырехугольной призмы; б) треугольной призмы; в) треугольной пирамиды? | | а) четырехугольной призмы; б) треугольной призмы; в) треугольной пирамиды? |
| | | | |
| - | <br>[[Image:21-07-109.jpg|480px|Задание]] <br><br>756. Из ружья сделано 50 выстрелов, при этом 5 пуль пролетели мимо цели. Определите процент попаданий. | + | <br>[[Image:21-07-109.jpg|480px|Задание]] <br><br>756. Из ружья сделано 50 выстрелов, при этом 5 пуль пролетели мимо цели. Определите '''[[Презентація уроку на тему «Відсоткове відношення»|процент попаданий]]'''. |
| | | | |
| | 757.Угол А равен 30°, а угол В равен 50°. Какую часть угол А составляет от угла В? Во сколько раз угол В больше угла А? | | 757.Угол А равен 30°, а угол В равен 50°. Какую часть угол А составляет от угла В? Во сколько раз угол В больше угла А? |
Текущая версия на 13:01, 7 октября 2012
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Пропорции
21. Пропорции
Отношения 3,6:1,2 и 6,3:2,1 равны, так как значения частных равны 3. Поэтому можно записать равенство 3,6:1,2 = 6,3:2,1, или 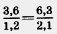
Равенство двух отношений называют пропорцией.
С помощью букв пропорцию записывают так: a:b = c:d или 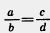
Эти записи читают так: «Отношение а к b равно отношению с к d>> или «а так относится к b, как с относится к d>>.
В пропорции 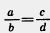 , или a:b=c:d, , или a:b=c:d,
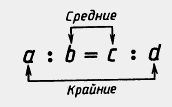
Числа a и d называют крайними членами, a числа b и с — средними членами пропорции. В дальнейшем будем считать, что все члены пропорции отличны от нуля: 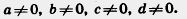 . .
В пропорции 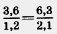 найдем произведение ее крайних и произведение ее средних членов. найдем произведение ее крайних и произведение ее средних членов.
Получим 3,6 • 2,1 = 7,56; 1,2 • 6,3 = 7,56. Значит, 3,6 • 2,1 = 1,2 • 6,3.
В верной пропорции произведение крайних членов равно произведению средних. Верно и обратное утверждение: если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна.
Это свойство называют основным свойством пропорции.
Пропорция 20:16 = 5:4 верна, так как 20 • 4 = 16 • 5 = 80. Поменяем местами в этой пропорции средние члены.
Получим новую пропорцию: 20:5 = 16:4. Она тоже верна, так как при такой перестановке произведение крайних и произведение средних членов не изменилось. Эти произведения не изменятся, если в пропорции 20:5 = 16:4 поменять местами крайние члены.
Если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны.
Используя основное свойство пропорции, можно найти ее неизвестный член, если все остальные члены известны.
Пример 1. Найдем в пропорции 0,5: а = 2:13 неизвестный средний член а.
Решение. Используя основное свойство пропорции, получим а • 2 = 0,5 • 13. Отсюда 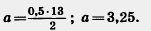
Пример 2. Решим уравнение 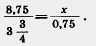
Решение. Используя основное свойство пропорции, получим 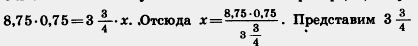 в виде десятичной дроби 3,75 и сократим выражение на 0,75, 8 75 в виде десятичной дроби 3,75 и сократим выражение на 0,75, 8 75
имеем 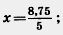 ; х= 1,75. ; х= 1,75.
? Что такое пропорция? Как называются числа х и у в пропорции х:а = b:у? Как называются числа x и y в пропорции x:y = a:b? Сформулируйте основное свойство пропорции. Какие перестановки членов пропорции снова приводят к верным пропорциям? Останется ли пропорция верной, если поменять местами какой-нибудь средний ее член с одним из крайних? Приведите пример. Останется ли пропорция верной, если оба средних члена поменять местами с крайними членами? Проверьте ваш ответ на пропорции 3:4 = 9:12.
К 744. Запишите пропорцию:
а) 5 так относится к 3, как 2 относится к 1,2;
б) 0,9 так относится к 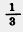 , как 45 относится к 16 , как 45 относится к 16 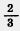
в) отношение 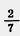 к 0,1 равно отношению 14 к 4,9. к 0,1 равно отношению 14 к 4,9.
Проверьте полученные пропорции, определяя отношения чисел.
745. Из каких отношений 0,6:5; 4,2:7; 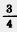 :6,25 можно составить верную пропорцию? :6,25 можно составить верную пропорцию?
746. Прочитайте пропорции и проверьте, верные ли они, используя основное свойство пропорции:
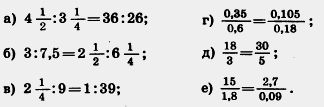
747. Решите уравнение:
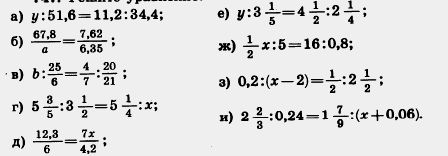
748. Переставив средние или крайние члены пропорции, составьте три новые верные пропорции из пропорции:
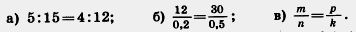
749. Используя верное равенство 4 • 9=0,2 • 180, составьте четыре верные пропорции.
П 750. Вычислите устно:
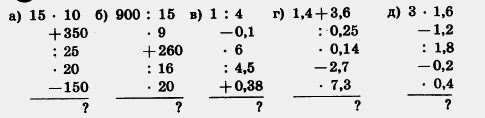
751. Какой знак действия надо подставить вместо *, чтобы получилось верное равенство:
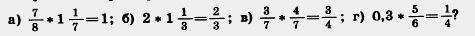
752. Найдите отношение величин:
а) 1,5 м и 30 см;
б) 1 кг и 250 г;
в) 1 ч и 15 мин;
г) 50 см2 и 1 дм2.
753. 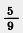 числа равны числа равны 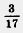 этого числа. Какое это число? этого числа. Какое это число?
754. Какое число надо прибавить к числителю и знаменателю дроби 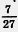 , чтобы получить дробь , чтобы получить дробь 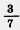 ? ?
М 755. Какие из фигур (рис. 33) являются развертками:
а) четырехугольной призмы; б) треугольной призмы; в) треугольной пирамиды?
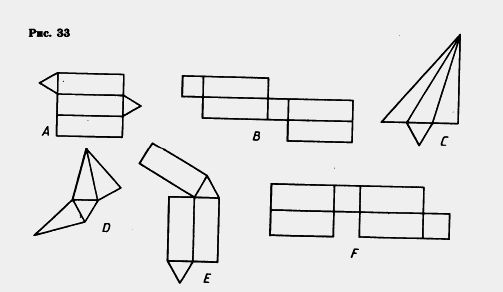
756. Из ружья сделано 50 выстрелов, при этом 5 пуль пролетели мимо цели. Определите процент попаданий.
757.Угол А равен 30°, а угол В равен 50°. Какую часть угол А составляет от угла В? Во сколько раз угол В больше угла А?
758. Бригаде было дано задание собрать 280 ц винограда. Она собрала 350 ц. На сколько процентов бригада перевыполнила задание? На сколько процентов бригада выполнила задание?
759.В парке посадили клены и дубы, причем на каждые 4 клена приходится один дуб. Сколько процентов от всех посаженных деревьев составляют клены? Сколько всего посадили деревьев в парке, если кленов посадили 480?
Д 760. Верна ли пропорция:
а) 2,04:0,6 = 2,72:0,8; б) 0,0112:0,28=0,204:0,51?
761. Решите уравнение:
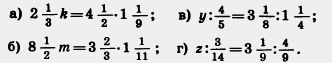
762. Из 225 кг руды получили 34,2 кг меди. Каково процентное содержание меди в руде?
763. Через 2 ч после выхода со станции А тепловоз увеличил скорость на 12 км/ч и через 5 ч после начала движения прибыл в пункт назначения В. Какова была скорость тепловоза в начале пути, если расстояние от А до В равно 261 км?
764. Если к 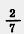 неизвестного числа прибавить 0,8, то получится 1,2. Найдите неизвестное число. неизвестного числа прибавить 0,8, то получится 1,2. Найдите неизвестное число.
765. Выполните действия:
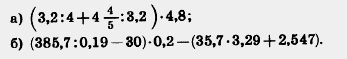
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|