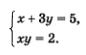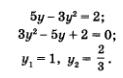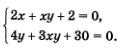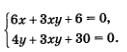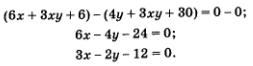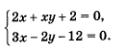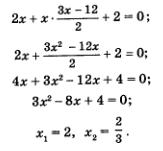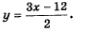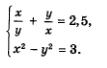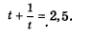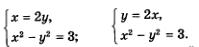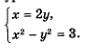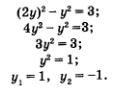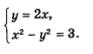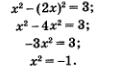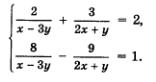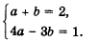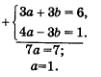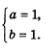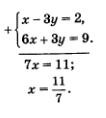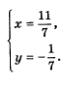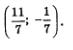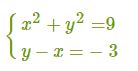|
|
|
| (6 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Методы решения систем уравнений<metakeywords>Методы решения систем уравнений</metakeywords>''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Методы решения систем уравнений<metakeywords>Методы решения систем уравнений, систем уравнений, алгоритмом, Переменные, уравнение, алгебраического сложения, рациональных уравнений, методом подстановки, иррациональных</metakeywords>''' |
| | | | |
| - | <br> | + | <h2>Какие существуют методы решения систем уравнения?</h2> |
| | | | |
| - | '''МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ'''<br>
| + | В этом параграфе мы обсудим три метода решения [[Системы уравнений. Основные понятия|систем уравнений]], более надежные, чем графический метод, который рассмотрели в предыдущем параграфе. |
| | | | |
| - | <br>В этом параграфе мы обсудим три метода решения систем уравнений, более надежные, чем графический метод, который рассмотрели в предыдущем параграфе.<br>'''1. Метод подстановки'''<br>Этот метод мы применяли в 7-м классе для решения систем линейных уравнений. Тот алгоритм, который был выработан в 7-м классе, вполне пригоден для решения систем любых двух уравнений (не обязательно линейных) с двумя переменными х и у (разумеется, переменные могут быть обозначены и другими буквами, что не имеет значения). Фактически этим алгоритмом мы воспользовались в предыдущем параграфе, когда задача о двузначном числе привела к математической модели, представляющей собой систему уравнений. Эту систему уравнений мы решили выше методом подстановки (см. пример 1 из § 4).<br>'''''Алгоритм использования метода подстановки при решении системы двух уравнений с двумя переменными х, у.'''''<br>'''1.''' Выразить у через х из одного уравнения системы.<br>'''2.''' Подставить полученное выражение вместо у в другое уравнение системы.<br>'''3.''' Решить полученное уравнение относительно х.<br>'''4.''' Подставить поочередно каждый из найденных на третьем шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.<br>'''5.''' Записать ответ в виде пар значений (х; у), которые были найдены соответственно на третьем и четвертом шаге.<br>Переменные х и у, разумеется, равноправны, поэтому с таким же успехом мы можем на первом шаге алгоритма выразить не у через х, а х через у из одного уравнения. Обычно выбирают то уравнение, которое представляется более простым, и выражают ту переменную из него, для которой эта процедура представляется более простой.<br>'''Пример 1.''' Решить систему уравнений [[Image:al61.jpg]]<br>'''Р е ш е н и е. 1)''' Выразим х через у из первого уравнения системы: х = 5 - 3у.<br>'''2) ''' Подставим полученное выражение вместо х во второе уравнение системы: (5 - 3у) у — 2.<br>'''3) ''' Решим полученное уравнение: [[Image:al62.jpg]]<br>'''4)''' Подставим поочередно каждое из найденных значений у в формулу х = 5 - Зу. Если [[Image:al63.jpg]] то [[Image:al64.jpg]]<br>'''5)''' Пары (2; 1) и [[Image:al65.jpg]] решения заданной системы уравнений. | + | <h2>Метод подстановки</h2> |
| | | | |
| - | '''О тв е т:''' (2; 1); [[Image:al65.jpg]]<br>'''2. Метод алгебраического сложения'''<br>Этот метод, как и метод подстановки, знаком вам из курса алгебры 7-го класса, где он применялся для решения систем линейных уравнений. Суть метода напомним на следующем примере.<br>'''Пример 2.''' Решить систему уравнений [[Image:al66.jpg]]<br>'''Решение.''' Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения: [[Image:al67.jpg]]<br>Вычтем второе уравнение системы из ее первого уравнения:
| + | Этот метод мы применяли в 7-м классе для решения систем линейных уравнений. Тот алгоритм, который был выработан в 7-м классе, вполне пригоден для решения систем любых двух уравнений (не обязательно линейных) с двумя переменными х и у (разумеется, переменные могут быть обозначены и другими буквами, что не имеет значения). Фактически этим [[Урок 4. Программа действий. Алгоритм|алгоритмом]] мы воспользовались в предыдущем параграфе, когда задача о двузначном числе привела к математической модели, представляющей собой систему уравнений. Эту систему уравнений мы решили выше методом подстановки (см. пример 1 из § 4). |
| | | | |
| - | [[Image:al68.jpg]]<br>В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой: [[Image:al69.jpg]]<br>Эту систему можно решить методом подстановки. Из второго уравнения находим [[Image:al610.jpg]] Подставив это выражение вместо у в первое уравнение системы, получим
| + | Алгоритм использования метода подстановки при решении системы двух уравнений с двумя переменными х, у. |
| | | | |
| - | [[Image:al611.jpg]]<br>Осталось подставить найденные значения х в формулу [[Image:al612.jpg]]
| + | 1. Выразить у через х из одного уравнения системы.<br>2. Подставить полученное выражение вместо у в другое уравнение системы.<br>3. Решить полученное уравнение относительно х.<br>4. Подставить поочередно каждый из найденных на третьем шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.<br>5. Записать ответ в виде пар значений (х; у), которые были найдены соответственно на третьем и четвертом шаге. |
| | | | |
| - | Если х = 2, то [[Image:al613.jpg]]<br>Таким образом, мы нашли два решения системы: [[Image:al614.jpg]]
| + | [[Линейное уравнение с двумя переменными и его график|Переменные]] х и у, разумеется, равноправны, поэтому с таким же успехом мы можем на первом шаге алгоритма выразить не у через х, а х через у из одного уравнения. Обычно выбирают то уравнение, которое представляется более простым, и выражают ту переменную из него, для которой эта процедура представляется более простой. |
| | | | |
| - | '''Ответ:''' [[Image:al615.jpg]] | + | '''Пример 1.''' Решить систему уравнений |
| | | | |
| - | '''3. Метод введения новых переменных'''<br>С методом введения новой переменной при решении рациональных уравнений с одной переменной вы познакомились в курсе алгебры 8-го класса. Суть этого метода при решении систем уравнений та же самая, но с технической точки зрения имеются некоторые особенности, которые мы и обсудим в следующих примерах.<br>Пример 3. Решить систему уравнений<br>— + — = 2,5, У х<br>х2 - у2 = 3.<br>х<br>Решение. Введем новую переменную *--• Тогда первое<br>У<br>уравнение системы можно будет переписать в более простом виде: Ь + ~ = 2,5. Решим это уравнение относительно переменной I:<br>I 2<br>2;2 + 2 - ы _ л 21<br>2*2 -5* +2 = 0;<br>Оба эти значения удовлетворяют условию 21Ф 0, а потому являются корнями рационального уравнения с переменной I.<br>X X<br>Но I = - , значит, либо — = 2, откуда находим, что х = 2у, либо У У<br>х 1<br>— = - , откуда находим, что у = 2х. У 2<br>Таким образом, с помощью метода введения новой переменной нам удалось как бы «расслоить» первое уравнение системы, достаточно сложное по виду, на два более простых уравнения:<br>х=2у; у — 2х.<br>
| + | [[Image:Al61.jpg|120px|Система уравнений]] |
| | | | |
| - | Что же дальше? А дальше каждое из двух полученных простых уравнений нужно поочередно рассмотреть в системе с уравнением х2 - у2 = 3, о котором мы пока не вспоминали. Иными словами, задача сводится к решению двух систем уравнений:<br>50<br>2.5.<br>СИСТЕМЫ УРАВНЕНИИ<br>х = 2 у, Г у = 2х,<br>х2 - у2 = 3; \х2 - у2 = 3. Надо найти решения первой системы, второй системы и все полученные пары значений включить в ответ. Решим первую систему уравнений:<br>х = 2 у, х2 - у2 = 3.<br>Воспользуемся методом подстановки, тем более что здесь для него все готово: подставим выражение 2у вместо х во второе уравнение системы. Получим<br>(2у)2-у2 = 3; 4 У2 - у2 —3; Зу2 = 3; У2 = 1; 2/1 = !> У2 = -1-<br>Так как х = 2у, то находим соответственно хх = 2, х2 = -2. Тем самым получены два решения заданной системы: (2; 1) и (-2; -1). Решим вторую систему уравнений:<br>у = 2х,<br>х2 - у2 = 3.<br>Снова воспользуемся методом подстановки: подставим выражение 2х вместо у во второе уравнение системы. Получим<br>х2-(2х)2 = 3; х2 -4.x2 = 3; -Зх2 = 3; х2 = -1.<br>Это уравнение не имеет корней, значит, и система уравнений не имеет решений. Таким образом, в ответ надо включить только решения первой системы.<br>Ответ: (2; 1); (-2;-1).<br>Метод введения новых переменных при решении систем двух уравнений с двумя переменными применяется в двух вариантах. Первый вариант: вводится одна новая переменная и используется только в одном<br>4*<br>51<br>2.6. I<br>СИСТЕМЫ УРАВНЕНИЙ<br>уравнении системы. Именно так обстояло дело в примере 3. Второй вариант: вводятся две новые переменные и используются одновременно в обоих уравнениях системы. Так будет обстоять дело в примере 4.<br>Пример 4. Решить систему уравнений 2 3<br>х-3у 8<br>2 х + у 9<br>= 2, = 1.<br>х-3у 2 х + у Решение. Введем две новые переменные: а =<br>6 =<br>Учтем, что тогда<br>8<br>х-3 у<br>- 4а,<br>= 36.<br>2х + у ' х-Зу " ' х ~ Зу<br>Это позволит переписать заданную систему в значительно более простом виде, но относительно новых переменных а и Ь:<br>\а + Ь = 2,<br>[4а - 36 = 1.<br>Применим для решения этой системы метод алгебраического сложения:<br>ГЗа + ЗЬ = 6, [4а- 36 = 1.<br>7а =7; а=1.<br>Так как а = 1, то из уравнения а + 6 = 2 находим: 1 + 6 = 2; 6=1. Таким образом, относительно переменных а и 6 мы получили одно решение:<br>[а = 1, [6 = 1.<br>Возвращаясь к переменным х и у, получаем систему уравнений<br>2<br>х-3у 3<br>2х + у<br>= 1, = 1,<br>т.е.<br>х-3 у = 2, 2х + у = 3.<br>52<br>2.6. I<br>СИСТЕМЫ УРАВНЕНИЙ<br>Применим для решения этой системы метод алгебраического сложения:<br>+ Г*-3 у-2, [6х + 3у = 9.<br>7х = 11; 11<br>11<br>И 7 22<br>Так как х = у, то из уравнения 2* + у = 3 находим: у~3-2х =<br>= 3-2-у=3- ?<br>Таким образом, относительно перемен-<br>ных хиу мы получили одно решение:<br>11<br>1<br><br>Ответ:<br>Г11 1<br>7 ' 7<br>обратите внимание<br>равносильность систем уравнений<br>Завершим этот параграф кратким, но достаточно серьезным теоретическим разговором. Вы уже накопили некоторый опыт в решении различных уравнений: линейных, квадратных, рациональных, иррациональных. Вы знаете, что основная идея решения уравнения состоит в постепенном переходе от одного уравнения к другому, более простому, но равносильному заданному. В предыдущем параграфе мы ввели понятие равносильности для уравнений с двумя переменными. Используют это понятие и для систем уравнений.<br>Определение. Две системы уравнений с переменными х и у называют равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.<br>Все три метода (подстановки, алгебраического сложения и введения новых переменных), которые<br>53<br>
| + | '''Решение. ''' |
| | | | |
| - | 2.6. I<br>СИСТЕМЫ УРАВНЕНИЙ<br>мы обсудили в этом параграфе, абсолютно корректны с точки зрения равносильности. Иными словами, используя эти методы, мы заменяем одну систему уравнений другой, более простой, но равносильной первоначальной системе.<br>
| + | 1) Выразим х через у из первого уравнения системы: х = 5 - 3у.<br>2)Подставим полученное выражение вместо х во второе уравнение системы: (5 - 3у) у — 2.<br>3)Решим полученное [[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнение]]: |
| | | | |
| - | <br> | + | [[Image:Al62.jpg|160px|Система уравнений]]<br>4) Подставим поочередно каждое из найденных значений у в формулу х = 5 - Зу. Если [[Image:Al63.jpg]] то [[Image:Al64.jpg|120px|Уравнение]]<br>5) Пары (2; 1) и [[Image:Al65.jpg]] решения заданной системы уравнений. |
| | | | |
| - | А.Г. Мордкович Алгебра 9 класс
| + | Ответ: (2; 1); [[Image:Al65.jpg]] |
| | | | |
| | + | <h2>Метод алгебраического сложения</h2> |
| | + | |
| | + | Этот метод, как и метод подстановки, знаком вам из курса алгебры 7-го класса, где он применялся для решения систем линейных уравнений. Суть метода напомним на следующем примере. |
| | + | |
| | + | '''Пример 2.''' Решить систему уравнений |
| | + | |
| | + | [[Image:Al66.jpg|160px|Система уравнений]]<br>'''Решение.''' |
| | + | |
| | + | Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения: [[Image:Al67.jpg|160px|Система уравнений]]<br>Вычтем второе уравнение системы из ее первого уравнения: |
| | + | |
| | + | [[Image:Al68.jpg|240px|Система уравнений]]<br>В результате [[Метод алгебраического сложения|алгебраического сложения]] двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой: |
| | + | |
| | + | [[Image:Al69.jpg|160px|Система уравнений]]<br>Эту систему можно решить методом подстановки. Из второго уравнения находим [[Image:Al610.jpg|Уравнение]] Подставив это выражение вместо у в первое уравнение системы, получим |
| | + | |
| | + | [[Image:Al611.jpg|240px|Система уравнений]]<br>Осталось подставить найденные значения х в формулу [[Image:Al612.jpg|120px|Формула]] |
| | + | |
| | + | Если х = 2, то |
| | + | |
| | + | [[Image:Al613.jpg|320px|Решение]]<br>Таким образом, мы нашли два решения системы: [[Image:Al614.jpg|120px|Решение]] |
| | + | |
| | + | Ответ: [[Image:Al615.jpg|120px|Ответ]] |
| | + | |
| | + | |
| | + | <h2>Метод введения новых переменных</h2> |
| | + | |
| | + | С методом введения новой переменной при решении [[Рациональные уравнения|рациональных уравнений]] с одной переменной вы познакомились в курсе алгебры 8-го класса. Суть этого метода при решении систем уравнений та же самая, но с технической точки зрения имеются некоторые особенности, которые мы и обсудим в следующих примерах. |
| | + | |
| | + | '''Пример 3.''' Решить систему уравнений |
| | + | |
| | + | [[Image:Al616.jpg|120px|Система уравнений]] |
| | + | |
| | + | '''Решение.''' Введем новую переменную [[Image:Al617.jpg]] Тогда первое уравнение системы можно будет переписать в более простом виде: [[Image:Al618.jpg|120px|Уравнение]] Решим это уравнение относительно переменной t: |
| | + | |
| | + | [[Image:Al619.jpg|160px|Решение]]<br>Оба эти значения удовлетворяют условию [[Image:Al620.jpg]], а потому являются корнями рационального уравнения с переменной t. Но [[Image:Al621.jpg]] значит, либо [[Image:Al622.jpg]] откуда находим, что х = 2у, либо [[Image:Al623.jpg]]<br>Таким образом, с помощью метода введения новой переменной нам удалось как бы «расслоить» первое уравнение системы, достаточно сложное по виду, на два более простых уравнения: |
| | + | |
| | + | х = 2 у; у — 2х.<br> |
| | + | |
| | + | Что же дальше? А дальше каждое из двух полученных простых уравнений нужно поочередно рассмотреть в системе с уравнением х<sup>2</sup> - у<sup>2</sup> = 3, о котором мы пока не вспоминали. Иными словами, задача сводится к решению двух [[Системи рівнянь з двома змінними. Графічний спосіб розв’язання систем рівнянь з двома змінними|систем уравнений]]: |
| | + | |
| | + | [[Image:Al624.jpg|240px|Система уравнений]] |
| | + | |
| | + | Надо найти решения первой системы, второй системы и все полученные пары значений включить в ответ. Решим первую систему уравнений: |
| | + | |
| | + | [[Image:Al625.jpg|120px|Система уравнений]]<br>Воспользуемся методом подстановки, тем более что здесь для него все готово: подставим выражение 2у вместо х во второе уравнение системы. Получим |
| | + | |
| | + | [[Image:Al626.jpg|160px|Система уравнений]]<br>Так как х = 2у, то находим соответственно х<sub>1</sub> = 2, х<sub>2</sub> = 2. Тем самым получены два решения заданной системы: (2; 1) и (-2; -1). Решим вторую систему уравнений: |
| | + | |
| | + | [[Image:Al627.jpg|120px|Система уравнений]]<br>Снова воспользуемся [[Метод подстановки|методом подстановки]]: подставим выражение 2х вместо у во второе уравнение системы. Получим |
| | + | |
| | + | [[Image:Al628.jpg|120px|Решение]]<br>Это уравнение не имеет корней, значит, и система уравнений не имеет решений. Таким образом, в ответ надо включить только решения первой системы. |
| | + | |
| | + | Ответ: (2; 1); (-2;-1). |
| | + | |
| | + | Метод введения новых переменных при решении систем двух уравнений с двумя переменными применяется в двух вариантах. Первый вариант: вводится одна новая переменная и используется только в одном уравнении системы. Именно так обстояло дело в примере 3.Второй вариант: вводятся две новые переменные и используются одновременно в обоих уравнениях системы. Так будет обстоять дело в примере 4. |
| | + | |
| | + | '''Пример 4.''' Решить систему уравнений |
| | + | |
| | + | [[Image:Al629.jpg|160px|Система уравнений]] |
| | + | |
| | + | '''Решение.''' |
| | + | |
| | + | Введем две новые переменные: |
| | + | |
| | + | [[Image:Al630.jpg|160px|Решение]] |
| | + | |
| | + | Учтем, что тогда |
| | + | |
| | + | [[Image:Al631.jpg|160px|Система уравнений]] |
| | + | |
| | + | Это позволит переписать заданную систему в значительно более простом виде, но относительно новых переменных а и b: |
| | + | |
| | + | [[Image:Al632.jpg|120px|Система уравнений]]<br>Применим для решения этой системы метод алгебраического сложения: |
| | + | |
| | + | [[Image:Al633.jpg|120px|Система уравнений]]<br>Так как а = 1, то из уравнения а + 6 = 2 находим: 1 + 6 = 2; 6=1. Таким образом, относительно переменных а и b мы получили одно решение: |
| | + | |
| | + | [[Image:Al634.jpg|Решение]]<br>Возвращаясь к переменным х и у, получаем систему уравнений |
| | + | |
| | + | [[Image:Al635.jpg|240px|Система уравнений]]<br>Применим для решения этой системы метод алгебраического сложения: |
| | + | |
| | + | [[Image:Al636.jpg|120px|Решение]]<br>Так как [[Image:Al637.jpg]] то из уравнения 2x + y = 3 находим: [[Image:Al638.jpg|240px|Решение]]<br>Таким образом, относительно переменных х и у мы получили одно решение: |
| | + | |
| | + | [[Image:Al639.jpg|80px|Решение]]<br>'''Ответ:''' [[Image:Al640.jpg|80px|Ответ]]<br>Завершим этот параграф кратким, но достаточно серьезным теоретическим разговором. Вы уже накопили некоторый опыт в решении различных уравнений: линейных, квадратных, рациональных, [[Иррациональные уравнения|иррациональных]]. Вы знаете, что основная идея решения уравнения состоит в постепенном переходе от одного уравнения к другому, более простому, но равносильному заданному. В предыдущем параграфе мы ввели понятие равносильности для уравнений с двумя переменными. Используют это понятие и для систем уравнений. |
| | + | |
| | + | '''Определение.''' |
| | + | |
| | + | Две системы уравнений с переменными х и у называют равносильными, если они имеют одни и те же решения или если обе системы не имеют решений. |
| | + | |
| | + | Все три метода (подстановки, алгебраического сложения и введения новых переменных), которые мы обсудили в этом параграфе, абсолютно корректны с точки зрения равносильности. Иными словами, используя эти методы, мы заменяем одну систему уравнений другой, более простой, но равносильной первоначальной системе.<br> |
| | + | |
| | + | <h2>Графический метод решения систем уравнений</h2> |
| | + | |
| | + | Мы уже с вами научились решать системы уравнений такими распространенными и надежными способами, как метод подстановки, алгебраического сложения и введения новых переменных. А теперь давайте с вами вспомним, метод, который вы уже изучали на предыдущем уроке. То есть давайте повторим, что вы знаете о графическом методе решения. |
| | + | |
| | + | Метод решения систем уравнения графическим способом представляет собой построение |
| | + | графика для каждого из конкретных уравнений, которые входят в данную систему и находятся в одной координатной плоскости, а также где требуется найти пересечения точек этих графиков. Для решения данной системы уравнений являются координаты этой точки (x; y). |
| | + | |
| | + | Следует вспомнить, что для графической системы уравнений свойственно |
| | + | иметь либо одно единственное верное решение, либо бесконечное множество решений, либо же не иметь решений вообще. |
| | + | |
| | + | А теперь на каждом из этих решений остановимся подробнее. И так, система уравнений может иметь единственное решение в случае, если прямые, которые являются графиками уравнений системы, пересекаются. Если же эти прямые параллельны, то такая система уравнений абсолютно не имеет решений. В случае же совпадения прямых графиков уравнений системы, то тогда такая система позволяет найти множество решений. |
| | + | |
| | + | Ну а теперь давайте с вами рассмотрим алгоритм решения системы двух уравнений с 2-мя неизвестными графическим методом: |
| | + | |
| | + | • Во-первых, вначале мы с вами строим график 1-го уравнения;<br> |
| | + | • Вторым этапом будет построение графика, который относится ко второму уравнению;<br> |
| | + | • В-третьих, нам необходимо найти точки пересечения графиков.<br> |
| | + | • И в итоге мы получаем координаты каждой точки пересечения, которые и будут решением системы уравнений.<br> |
| | + | |
| | + | Давайте этот метод рассмотрим более подробно на примере. Нам дана система уравнений, которую необходимо решить: |
| | + | |
| | + | <br> |
| | + | [[Image:9kl_Graf_Metod01.jpg|200x500px|графический метод]] |
| | <br> | | <br> |
| | | | |
| - | <sub>Материалы по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, планы конспектов уроков по математике [[Математика|скачать]]</sub>
| + | '''Решение уравнений''' |
| | | | |
| - | '''<u>Содержание урока</u>'''
| + | 1. Вначале мы с вами будем строить график данного уравнения: x2+y2=9.<br> |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии
| + | |
| - |
| + | |
| - | '''<u>Практика</u>'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
| + | |
| - |
| + | |
| - | '''<u>Иллюстрации</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
| + | |
| - |
| + | |
| - | '''<u>Дополнения</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие
| + | |
| - |
| + | |
| - | <u>Совершенствование учебников и уроков
| + | |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми
| + | |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения
| + | |
| - |
| + | |
| - |
| + | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| | | | |
| | + | Но следует заметить, что данным графиком уравнений будет окружность, имеющая центр в начале координат, а ее радиус будет равен трем. |
| | + | |
| | + | 2. Следующим нашим шагом будет построение графика такого уравнения, как: |
| | + | y = x – 3.<br> |
| | + | |
| | + | В этом случае, мы должны построить прямую и найти точки (0;−3) и (3;0). |
| | + | |
| | + | <br> |
| | + | [[Image:9kl_Graf_Metod02.jpg|500x500px|графический метод]] |
| | <br> | | <br> |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | 3. Смотрим, что у нас получилось. Мы видим, что прямая пересекает окружность в двух ее точках A и B. <br> |
| | + | |
| | + | Теперь мы с вами ищем координаты этих точек. Мы видим, что координаты (3;0) соответствуют точке А, а координаты (0;−3) соответственно точке В. |
| | + | |
| | + | И что мы получаем в итоге? |
| | + | |
| | + | Получившиеся при пересечении прямой с окружностью числа (3;0) и (0;−3), как раз и являются решениями обоих уравнений системы. А из этого следует, что данные числа являются и решениями этой системы уравнений. |
| | + | |
| | + | То есть, ответом этого решения являются числа: (3;0) и (0;−3). |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | ''А.Г. Мордкович [http://xvatit.com/vuzi/ Алгебра] 9 класс'' |
Текущая версия на 11:35, 7 июля 2015
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Методы решения систем уравнений
Какие существуют методы решения систем уравнения?
В этом параграфе мы обсудим три метода решения систем уравнений, более надежные, чем графический метод, который рассмотрели в предыдущем параграфе.
Метод подстановки
Этот метод мы применяли в 7-м классе для решения систем линейных уравнений. Тот алгоритм, который был выработан в 7-м классе, вполне пригоден для решения систем любых двух уравнений (не обязательно линейных) с двумя переменными х и у (разумеется, переменные могут быть обозначены и другими буквами, что не имеет значения). Фактически этим алгоритмом мы воспользовались в предыдущем параграфе, когда задача о двузначном числе привела к математической модели, представляющей собой систему уравнений. Эту систему уравнений мы решили выше методом подстановки (см. пример 1 из § 4).
Алгоритм использования метода подстановки при решении системы двух уравнений с двумя переменными х, у.
1. Выразить у через х из одного уравнения системы.
2. Подставить полученное выражение вместо у в другое уравнение системы.
3. Решить полученное уравнение относительно х.
4. Подставить поочередно каждый из найденных на третьем шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.
5. Записать ответ в виде пар значений (х; у), которые были найдены соответственно на третьем и четвертом шаге.
Переменные х и у, разумеется, равноправны, поэтому с таким же успехом мы можем на первом шаге алгоритма выразить не у через х, а х через у из одного уравнения. Обычно выбирают то уравнение, которое представляется более простым, и выражают ту переменную из него, для которой эта процедура представляется более простой.
Пример 1. Решить систему уравнений
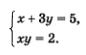
Решение.
1) Выразим х через у из первого уравнения системы: х = 5 - 3у.
2)Подставим полученное выражение вместо х во второе уравнение системы: (5 - 3у) у — 2.
3)Решим полученное уравнение:
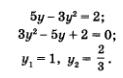
4) Подставим поочередно каждое из найденных значений у в формулу х = 5 - Зу. Если 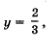 то то 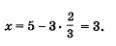
5) Пары (2; 1) и 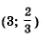 решения заданной системы уравнений. решения заданной системы уравнений.
Ответ: (2; 1); 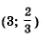
Метод алгебраического сложения
Этот метод, как и метод подстановки, знаком вам из курса алгебры 7-го класса, где он применялся для решения систем линейных уравнений. Суть метода напомним на следующем примере.
Пример 2. Решить систему уравнений
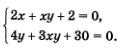
Решение.
Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения: 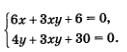
Вычтем второе уравнение системы из ее первого уравнения:
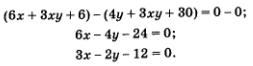
В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой:
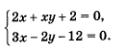
Эту систему можно решить методом подстановки. Из второго уравнения находим 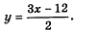 Подставив это выражение вместо у в первое уравнение системы, получим Подставив это выражение вместо у в первое уравнение системы, получим
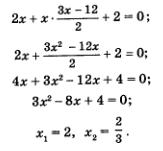
Осталось подставить найденные значения х в формулу 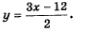
Если х = 2, то
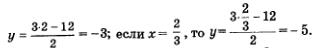
Таким образом, мы нашли два решения системы: 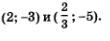
Ответ: 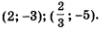
Метод введения новых переменных
С методом введения новой переменной при решении рациональных уравнений с одной переменной вы познакомились в курсе алгебры 8-го класса. Суть этого метода при решении систем уравнений та же самая, но с технической точки зрения имеются некоторые особенности, которые мы и обсудим в следующих примерах.
Пример 3. Решить систему уравнений
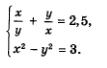
Решение. Введем новую переменную 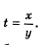 Тогда первое уравнение системы можно будет переписать в более простом виде: Тогда первое уравнение системы можно будет переписать в более простом виде: 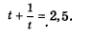 Решим это уравнение относительно переменной t: Решим это уравнение относительно переменной t:

Оба эти значения удовлетворяют условию  , а потому являются корнями рационального уравнения с переменной t. Но , а потому являются корнями рационального уравнения с переменной t. Но 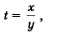 значит, либо значит, либо 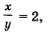 откуда находим, что х = 2у, либо откуда находим, что х = 2у, либо 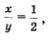
Таким образом, с помощью метода введения новой переменной нам удалось как бы «расслоить» первое уравнение системы, достаточно сложное по виду, на два более простых уравнения:
х = 2 у; у — 2х.
Что же дальше? А дальше каждое из двух полученных простых уравнений нужно поочередно рассмотреть в системе с уравнением х2 - у2 = 3, о котором мы пока не вспоминали. Иными словами, задача сводится к решению двух систем уравнений:
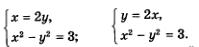
Надо найти решения первой системы, второй системы и все полученные пары значений включить в ответ. Решим первую систему уравнений:
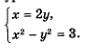
Воспользуемся методом подстановки, тем более что здесь для него все готово: подставим выражение 2у вместо х во второе уравнение системы. Получим
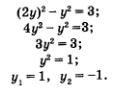
Так как х = 2у, то находим соответственно х1 = 2, х2 = 2. Тем самым получены два решения заданной системы: (2; 1) и (-2; -1). Решим вторую систему уравнений:
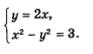
Снова воспользуемся методом подстановки: подставим выражение 2х вместо у во второе уравнение системы. Получим
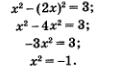
Это уравнение не имеет корней, значит, и система уравнений не имеет решений. Таким образом, в ответ надо включить только решения первой системы.
Ответ: (2; 1); (-2;-1).
Метод введения новых переменных при решении систем двух уравнений с двумя переменными применяется в двух вариантах. Первый вариант: вводится одна новая переменная и используется только в одном уравнении системы. Именно так обстояло дело в примере 3.Второй вариант: вводятся две новые переменные и используются одновременно в обоих уравнениях системы. Так будет обстоять дело в примере 4.
Пример 4. Решить систему уравнений
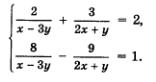
Решение.
Введем две новые переменные:
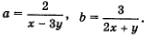
Учтем, что тогда
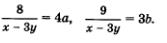
Это позволит переписать заданную систему в значительно более простом виде, но относительно новых переменных а и b:
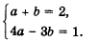
Применим для решения этой системы метод алгебраического сложения:
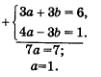
Так как а = 1, то из уравнения а + 6 = 2 находим: 1 + 6 = 2; 6=1. Таким образом, относительно переменных а и b мы получили одно решение:
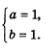
Возвращаясь к переменным х и у, получаем систему уравнений
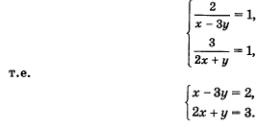
Применим для решения этой системы метод алгебраического сложения:
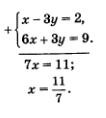
Так как 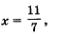 то из уравнения 2x + y = 3 находим: то из уравнения 2x + y = 3 находим: 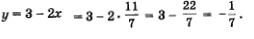
Таким образом, относительно переменных х и у мы получили одно решение:
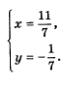
Ответ: 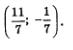
Завершим этот параграф кратким, но достаточно серьезным теоретическим разговором. Вы уже накопили некоторый опыт в решении различных уравнений: линейных, квадратных, рациональных, иррациональных. Вы знаете, что основная идея решения уравнения состоит в постепенном переходе от одного уравнения к другому, более простому, но равносильному заданному. В предыдущем параграфе мы ввели понятие равносильности для уравнений с двумя переменными. Используют это понятие и для систем уравнений.
Определение.
Две системы уравнений с переменными х и у называют равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.
Все три метода (подстановки, алгебраического сложения и введения новых переменных), которые мы обсудили в этом параграфе, абсолютно корректны с точки зрения равносильности. Иными словами, используя эти методы, мы заменяем одну систему уравнений другой, более простой, но равносильной первоначальной системе.
Графический метод решения систем уравнений
Мы уже с вами научились решать системы уравнений такими распространенными и надежными способами, как метод подстановки, алгебраического сложения и введения новых переменных. А теперь давайте с вами вспомним, метод, который вы уже изучали на предыдущем уроке. То есть давайте повторим, что вы знаете о графическом методе решения.
Метод решения систем уравнения графическим способом представляет собой построение
графика для каждого из конкретных уравнений, которые входят в данную систему и находятся в одной координатной плоскости, а также где требуется найти пересечения точек этих графиков. Для решения данной системы уравнений являются координаты этой точки (x; y).
Следует вспомнить, что для графической системы уравнений свойственно
иметь либо одно единственное верное решение, либо бесконечное множество решений, либо же не иметь решений вообще.
А теперь на каждом из этих решений остановимся подробнее. И так, система уравнений может иметь единственное решение в случае, если прямые, которые являются графиками уравнений системы, пересекаются. Если же эти прямые параллельны, то такая система уравнений абсолютно не имеет решений. В случае же совпадения прямых графиков уравнений системы, то тогда такая система позволяет найти множество решений.
Ну а теперь давайте с вами рассмотрим алгоритм решения системы двух уравнений с 2-мя неизвестными графическим методом:
• Во-первых, вначале мы с вами строим график 1-го уравнения;
• Вторым этапом будет построение графика, который относится ко второму уравнению;
• В-третьих, нам необходимо найти точки пересечения графиков.
• И в итоге мы получаем координаты каждой точки пересечения, которые и будут решением системы уравнений.
Давайте этот метод рассмотрим более подробно на примере. Нам дана система уравнений, которую необходимо решить:
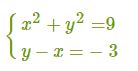
Решение уравнений
1. Вначале мы с вами будем строить график данного уравнения: x2+y2=9.
Но следует заметить, что данным графиком уравнений будет окружность, имеющая центр в начале координат, а ее радиус будет равен трем.
2. Следующим нашим шагом будет построение графика такого уравнения, как:
y = x – 3.
В этом случае, мы должны построить прямую и найти точки (0;−3) и (3;0).
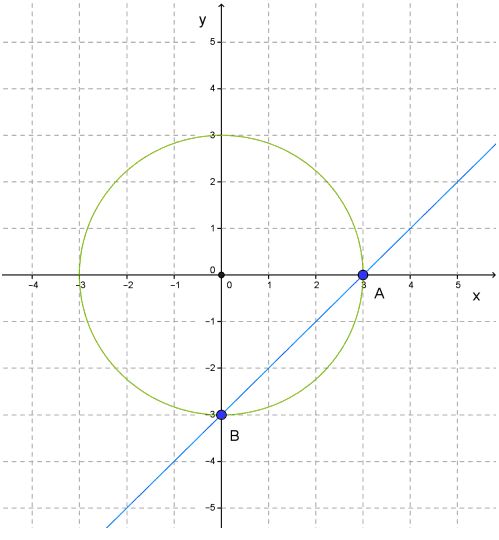
3. Смотрим, что у нас получилось. Мы видим, что прямая пересекает окружность в двух ее точках A и B.
Теперь мы с вами ищем координаты этих точек. Мы видим, что координаты (3;0) соответствуют точке А, а координаты (0;−3) соответственно точке В.
И что мы получаем в итоге?
Получившиеся при пересечении прямой с окружностью числа (3;0) и (0;−3), как раз и являются решениями обоих уравнений системы. А из этого следует, что данные числа являются и решениями этой системы уравнений.
То есть, ответом этого решения являются числа: (3;0) и (0;−3).
А.Г. Мордкович Алгебра 9 класс
|