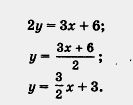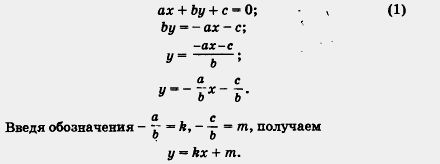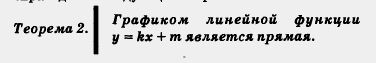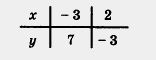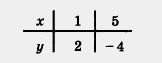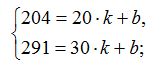|
|
|
| (7 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Линейная функция, ее график</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Линейная функция, ее график, уравнение, таблицы, натуральное число, координатная плоскость, математические модели, переменная</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Линейная функция и ее график''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Линейная функция и ее график ''' |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <br>''' ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК''' | + | <h2>Линейная функция и ее график</h2> |
| | | | |
| - | <br>Алгоритм построения графика уравнения ах + by + с = 0, который мы сформулировали в § 28, при всей его четкости и определенности математикам не очень нравится. Обычно они выдвигают претензии к первым двум шагам алгоритма. Зачем, говорят они, дважды решать уравнение относительно переменной у: <br>сначала ах1 + Ьу + с = О, затем ахг + Ьу + с = О? Не лучше ли сразу выразить у из уравнения ах + by + с = 0, тогда легче будет проводить вычисления (и, главное, быстрее)? Давайте проверим. Рассмотрим сначала уравнение 3x - 2у + 6 = 0 (см. пример 2 из § 28). | + | '''<br> '''Алгоритм построения графика уравнения ах + by + с = 0, который мы сформулировали в § 28, при всей его четкости и определенности математикам не очень нравится. Обычно они выдвигают претензии к первым двум шагам алгоритма. Зачем, говорят они, дважды решать уравнение относительно переменной у: сначала ах1 + Ьу + с = О, затем ахг + Ьу + с = О? Не лучше ли сразу выразить у из уравнения ах + by + с = 0, тогда легче будет проводить вычисления (и, главное, быстрее)? Давайте проверим. Рассмотрим сначала '''[[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнение]]''' 3x - 2у + 6 = 0 (см. пример 2 из § 28). |
| | | | |
| | Имеем: | | Имеем: |
| | | | |
| - | [[Image:09-06-20.jpg]]<br><br>Придавая х конкретные значения, легко вычислить соответствующие значения у. Например, при х = 0 получаем у = 3; при х = -2 имеем у = 0; при х = 2 имеем у = 6; при х = 4 получаем: у = 9. | + | [[Image:09-06-20.jpg|180px|Уравнения]]<br><br>Придавая х конкретные значения, легко вычислить соответствующие значения у. Например, при х = 0 получаем у = 3; при х = -2 имеем у = 0; при х = 2 имеем у = 6; при х = 4 получаем: у = 9. |
| | | | |
| | Видите, как легко и быстро найдены точки (0; 3), (- 2; 0), (2; 6) и (4; 9), которые были выделены в примере 2 из § 28. | | Видите, как легко и быстро найдены точки (0; 3), (- 2; 0), (2; 6) и (4; 9), которые были выделены в примере 2 из § 28. |
| | | | |
| - | Точно так же уравнение Ьх - 2у = 0 (см. пример 4 из § 28) можно было преобразовать к виду 2у =16 -3x . далее у = 2,5x; нетрудно найти точки (0; 0) и (2; 5), удовлетворяющие этому уравнению. <br>Наконец, уравнение 3x + 2у - 16 = 0 из того же примера можно преобразовать к виду 2y = 16 -3x и далее [[Image:09-06-21.jpg]] нетрудно найти точки (0; 0) и (2; 5), которые ему удовлетворяют. | + | Точно так же уравнение Ьх - 2у = 0 (см. пример 4 из § 28) можно было преобразовать к виду 2у =16 -3x . далее у = 2,5x; нетрудно найти точки (0; 0) и (2; 5), удовлетворяющие этому уравнению. <br> |
| | | | |
| - | Рассмотрим теперь указанные преобразования в общем виде. <br>Имеем:
| + | Наконец, уравнение 3x + 2у - 16 = 0 из того же примера можно преобразовать к виду 2y = 16 -3x и далее [[Image:09-06-21.jpg|90px|Уравнение]] нетрудно найти точки (0; 0) и (2; 5), которые ему удовлетворяют. |
| | | | |
| - | [[Image:09-06-22.jpg]]<br>
| + | Рассмотрим теперь указанные преобразования в общем виде. <br> |
| | | | |
| - | Таким образом, линейное уравнение (1) с двумя переменными хиу всегда можно преобразовать к виду <br>y = kx + m,(2) <br>где k,m — числа (коэффициенты), причем [[Image:09-06-23.jpg]]. | + | Имеем: |
| | + | |
| | + | [[Image:09-06-22.jpg|480px|Линейное уравнение]]<br> |
| | + | |
| | + | Таким образом, линейное уравнение (1) с двумя переменными х и у всегда можно преобразовать к виду <br>y = kx + m,(2) где k,m — числа (коэффициенты), причем [[Image:09-06-23.jpg|40px|k не равно 0]]. |
| | + | |
| | + | Этот частный вид линейного уравнения будем называть линейной функцией. <br> |
| | | | |
| - | Этот частный вид линейного уравнения будем называть линейной функцией. <br>С помощью равенства (2) легко, указав конкретное значение х, вычислить соответствующее значение у. Пусть, например,
| + | С помощью равенства (2) легко, указав конкретное значение х, вычислить соответствующее значение у. Пусть, например, |
| | | | |
| | у = 2х + 3. Тогда: <br>если х = 0, то у = 3; <br>если х = 1, то у = 5; <br>если х = -1, то у = 1; <br>если х = 3, то у = 9 и т. д. | | у = 2х + 3. Тогда: <br>если х = 0, то у = 3; <br>если х = 1, то у = 5; <br>если х = -1, то у = 1; <br>если х = 3, то у = 9 и т. д. |
| | | | |
| - | Обычно эти результаты оформляют в виде таблицы: | + | Обычно эти результаты оформляют в виде '''[[Табличные информационные модели|таблицы]]''': |
| | | | |
| - | [[Image:09-06-24.jpg]]<br><br>Значения у из второй строки таблицы называют значениями линейной функции у = 2х + 3, соответственно, в точках х = 0, х = 1, х = -1,х=-3. <br>В уравнении (1) переменные хну равноправны, а в уравнении (2) — нет: конкретные значения мы придаем одной из них — переменной х, тогда как значение переменной у зависит от выбранного значения переменной х. Поэтому обычно говорят, что х — независимая переменная (или аргумент), у — зависимая переменная.
| + | <br> |
| | | | |
| - | <br>специальный вид линейного уравнения с двумя пе- <br>ременными. Графиком уравнения у — kx + т, как <br>всякого линейного уравнения с двумя переменны- <br>ми, является прямая — ее называют также графи- <br>ком линейной функции y = kx + тп. Таким образом, <br>справедлива следующая теорема. <br>Графиком линейной функции <br>у = kx + m является прямая. <br>Теорема 2. <br>Пример 1. Построить график линейной <br>функции у = 2х + 3. <br>Решение. Составим таблицу: <br>/ <br>У <br>к <br>3. <br>7 <br>/ <br>0 <br>| <br>]/ <br>/ <br>1 <br>/ <br>X <br>X <br>У <br>0 <br>3 <br>1 <br>5 <br>Рис. 36 <br>Построим на координатной плоскости хОу <br>точки @; 3) и A; 5) и проведем через них пря- <br>мую. Это и есть график линейной функции <br>у = 2х + 3 (рис. 36). <¦ <br>Замечание. В § 25 мы уже говорили о том, как <br>обстоит дело в математике с новыми понятиями, но- <br>выми терминами. Часто бывает так: ввели новое поня- <br>тие, работают с ним, но затем, по мере дальнейшего <br>изучения математики, начинают осознавать, что вве- <br>денное понятие требует уточнения, развития. Именно <br>так обстояло дело с понятием «тождество». Точно <br>так же обстоит дело и с понятием «функция». Мы <br>еще довольно долго будем привыкать к нему, наби- <br>раться опыта, работать с этим понятием пока не при- <br>дем к строгому определению (зто будет в 9 классе). <br>Многие реальные ситуации описываются математическими <br>моделями, представляющими собой линейные функции. Приве- <br>Приведем примеры. <br>ЛИНЕЙНАЯ ФУНКЦИЯ <br>Первая ситуация. На складе было 500 т угля. Ежедневно <br>стали подвозить по 30 т угля. Сколько угля будет на складе через <br>2, 4, 10 дней? <br>Если пройдет х дней, то количество у угля на складе (в тоннах) <br>выразится формулой у — 500 + ЗОд:. Таким образом, линейная фун- <br>кция у = ЗОд: + 500 есть математическая модель ситуации. <br>Теперь нетрудно установить, что: <br>при х = 2 имеем у = 560 (в уравнение у = ЗОд: + 500 подставили <br>х = 2 и получили у = 560); <br>при х = 4 имеем у = 620; <br>при х = 10 имеем у = 800. <br>Вторая ситуация. На складе было 500 т угля. Ежедневно <br>стали увозить по 30 т угля. Сколько угля будет на складе через 2, <br>4,10 дней? <br>Здесь математической моделью ситуации является линейная <br>функция у = 500 - ЗОд:. С помощью этой модели нетрудно отве- <br>тить на вопрос задачи: <br>если х = 2, то у = 440 (в уравнение у = 500 - ЗОд: подставили <br>х — 2 и получили у = 440); <br>если х = 4, то у = 380; <br>если х = 10, то у = 200. <br>Третья ситуация. Турист проехал на автобусе 15 км от <br>пункта А до Б, а затем продолжил движение из пункта В в том <br>же направлении, но уже пешком, со скоростью 4 км/ч. На каком <br>расстоянии от А будет турист через 2 ч, через 4 ч, через 5 ч <br>ходьбы? <br>Математической моделью ситуации является линейная функ- <br>ция у=15 + 4х, где х — время ходьбы (в часах), у — расстояние от А <br>(в километрах). С помощью этой модели отвечаем на вопрос задачи: <br>если х = 2, то у = 23 (в уравнение у = 15 + 4д: подставили х = 2 <br>и получили у = 23); <br>если д: = 4, то у = 31; <br>если х = 6, то у = 39. <br>На самом деле во всех математических моделях <br>этих трех ситуаций мы допустили неточности, по- <br>скольку ничего не сказали о тех ограничениях на <br>х, которые вытекают из смысла задачи. Ведь ясно, <br>что в первой ситуации независимая переменная х <br>114 <br>может принимать только значения 1, 2, 3, ..., поскольку х — <br>число дней. Следовательно, уточненная математическая модель <br>первой ситуации выглядит так: <br>у = 500 + ЗОд:, где х — натуральное число. <br>Во второй ситуации независимая переменная х, обозначаю- <br>щая, как и в первой ситуации, число дней, может принимать толь- <br>ко значения 1, 2, 3, ..., 16. Действительно, если х = 16, то по <br>формуле у = 500 - ЗОд: находим: у = 500 - 30 • 16 = 20. Значит, <br>уже на 17-й день вывезти со склада 30 т угля не удастся, посколь- <br>ку на складе к этому дню останется всего 20 т и процесс вывоза <br>угля придется прекратить. Следовательно, уточненная математи- <br>ческая модель второй ситуации выглядит так: <br>у = 500 - ЗОд:, где х = 1, 2, 3, .... 16. <br>В третьей ситуации независимая переменная х теоретически мо- <br>жет принять любое неотрицательное значение (напр., значение х = 0, <br>значение х = 2, значение х = 3,5 и т. д.), но практически турист не <br>может шагать с постоянной скоростью без сна и отдыха сколько <br>угодно времени. Значит, нам нужно было сделать разумные ограни- <br>чения на х, скажем, 0 < х < 6 (т. е. турист идет не более 6 ч). <br>Напомним, что геометрической моделью нестрогого двойного <br>неравег -тва 0 < х < 6 служит отрезок [0, 6] (рис. 37). Значит, уточ- <br>ненная модель третьей ситуации выглядит так: у = 15 + 4х, где х <br>принадлежит отрезку [0, 6]. <br>х <br>0 6 <br>Рис. 37 <br>Условимся вместо фразы *х принадлежит множеству X» <br>писать хт X (читают: «элемент х принадлежит множеству X», <br>е — знак принадлежности). Как видите, наше знакомство с матема- <br>тическим языком постоянно продолжается. <br>Если линейную функцию у = kx + m надо рассматривать не <br>при всех значениях х, а лишь для значений х из некоторого чис- <br>лового промежутка X, то пишут: <br>У <br>¦¦ kx + т, х е X. <br>Пример 2. Построить график линейной функции: <br>-2*+l, xe[-3,2]; <br>-2*+1, хе(-3,2). <br>Решение, а) Составим таблицу для линейной функции <br>X <br>У <br>-3 <br>7 <br>2 <br>-3 <br>Построим на координатной плоскости хОу точки (-3; 7) и <br>B; -3) и проведем через них прямую линию. Это — график урав- <br>нения у = -2д: + 1. Далее, выделим отрезок, соединяющий постро- <br>енные точки (рис. 38). Этот отрезок и есть график линейной фун- <br>кции у = -2х+1, гдехе [-3, 2]. <br>Обычно говорят так: мы построили график линейной функ- <br>ции у = - 2х + 1 на отрезке [- 3, 2]. <br>б) Чем отличается этот пример от предыдущего? Линейная <br>функция та же (у = -2х + 1), значит, и ее графиком служит та же <br>прямая. Но — будьте внимательны! — на этот раз х е (-3, 2), т. е. <br>значения х = -3 и х = 2 не рассматриваются, они не принадлежат <br>интервалу (- 3, 2). Как мы отмечали концы интервала на коорди- <br>-302* <br>Рис. 39 <br>-{ <br>\ <br>\ <br>¦1 <br>\ <br>\ <br>\ <br>0 <br>о <br>1 <br>у <br>\ <br>1 : <br>\ <br>X <br>| <br>\ <br>ч <br>N <br>\ <br>0 <br>\ _ <br>V <br>1 <br>у <br>\ <br>L : <br>\ <br>1 <br>1 <br>\ <br>X <br>t <br>к <br>yt <br>\ <br>\ <br>0 <br>о <br>I <br>1 <br>\ <br>V <br>X <br>Рис. 38 <br>Рис. 40 <br>Рис. 41 <br>117 <br>натной прямой? Светлыми кружочками (рис. 39), об этом мы го- <br>ворили в § 26. Точно так же и точки (- 3; 7) и B; - 3) придется <br>отметить на чертеже светлыми кружочками. Это будет напоми- <br>нать нам о том, что берутся лишь те точки прямой у = - 2х + 1, <br>которые лежат между точками, отмеченными кружочками <br>(рис. 40). Впрочем, иногда в таких случаях используют не свет- <br>лые кружочки, а стрелки (рис. 41). Это не- <br>принципиально, главное, понимать, о чем <br>идет речь. <И <br>Пример 3. Найти наибольшее и <br>наименьшее значения линейной функции <br>у = -г + 4 на отрезке [0, 6]. <br>Решение. Составим таблицу для ли- <br>нейной функции у—^ +4: <br>6 29 <br>4. <br>0 <br>1 <br>к* <br>1 <br>у <br>1 <br>V <br>1 <br>X <br>У <br>0 <br>4 <br>6 <br>7 <br>Рис. 42 <br>Построим на координатной плоскости хОу <br>точки @; 4) и F; 7) и проведем через них прямую — график линейной <br>х <br>функции у = -г + 4 (рис. 42). <br>Нам нужно рассмотреть эту линейную функцию <br>не целиком, а на отрезке [0, 6], т. е. для х е [0, 6]. <br>Соответствующий отрезок графика выделен на чер- <br>теже. Замечаем, что самая большая ордината у то- <br>чек, принадлежащих выделенной части, равна 7 — <br>это и есть наибольшее значение линейной функции <br>у — -z + 4 на отрезке [0, 6]. Обычно используют <br>такую запись: унаиб =7. <br>Отмечаем, что самая маленькая ордината у то- <br>чек, принадлежащих выделенной на рисунке 42 ча- <br>сти прямой, равна 4 — это и есть наименьшее значе- <br>х <br>ние линейной функции y=~z +4 на отрезке [0, 6]. <br>Обычно используют такую запись: г/наим. = 4. <br>Пример 4. Найти унаив- и уМт для линейной функции <br>у <br>а) на отрезке [1,5]; б) на интервале A,5); <br>в) на полуинтервале [1, 5); г) на луче [0, + со); <br>д) на луче (- со, 3]. <br>Решение. Составим таблицу для линейной функции <br>у = -l,5x + 3,5: <br>X <br>У <br>1 <br>2 <br>5 <br>-4 <br>Построим на координатной плоскости хОу точки A; 2) и E; - 4) <br>и проведем через них прямую (рис. 43-47). Выделим на построен- <br>ной прямой часть, соответствующую значениям х из отрезка [1,5] <br>(рис. 43), из интервала A, 5) (рис. 44), из полуинтервала [1, 5) <br>(рис. 45), из луча [0, + со) (рис. 46), из луча (- со, 3] (рис. 47). <br>а) С помощью рисунка 43 нетрудно сделать вывод, что унаиб = 2 <br>(этого значения линейная функция достигает при х = 1), а утим_ = - 4 <br>(этого значения линейная функция достигает при х = 5). <br>б) Используя рисунок 44, делаем вывод: ни наибольшего, <br>ни наименьшего значений на заданном интервале у данной ли- <br>нейной функции нет. Почему? Дело в том, что, в отличие от пре- <br>дыдущего случая, оба конца отрезка, в которых как раз и дости- <br>гались наибольшее и наименьшее значения, из рассмотрения ис- <br>ключены. <br>yi <br>о <br>0 <br>-4 <br>Л <br>\ <br>S <br>1 <br>\ <br>\ <br>5 <br>h <br>\ <br>\ <br>,5 <br>*-» <br>X <br>3, <br>5 <br>У <br>о <br>0 <br>-Л <br>\ <br>\ <br>1 <br>ч <br>\ <br>\ <br>-1 <br>5 <br>ъ <br>\ <br>,5 <br>К <br>з, <br>X <br>5 <br>Рис. 43 <br>Рис. 44 <br>118 <br>в) С помощью рисунка 45 заключаем, что г/наи6. = 2 (как и в <br>первом случае), а наименьшего значения у линейной функции <br>нет (как и во втором случае). <br>г) Используя рисунок 46, делаем вывод: утиб = 3,5 (этого значе- <br>ния линейная функция достигает при х = 0), а унаим. не существует. <br>д) С помощью рисунка 47 делаем вывод: y^^ = -1 (этого значе- <br>ния линейная функция достигает при х = 3), а ушиб, не существует. <br>Пример 5. Построить график линейной функции <br>у = 2х - 6. С помощью графика ответить на следующие вопросы: <br>а) при каком значении х будет у = 0? <br>б) при каких значениях х будет у > 0? <br>в) при каких значениях х будет у < 0? <br>Ре ш е ни е. Составим таблицу для линейной функции у = 2х- 6: <br>X <br>У <br>0 <br>-6 <br>3 <br>0 <br>Через точки @; - 6) и C; 0) проведем прямую — график функ- <br>ции у = 2х - 6 (рис. 48). <br>а) у = 0 при х = 3. График пересекает ось х в точке х = 3, это и <br>есть точка с ординатой у = 0. <br>б) у > 0 при х > 3. В самом деле если х > 3, то прямая располо- <br>жена выше оси ж, значит, ординаты соответствующих точек <br>прямой положительны. <br>расположена ниже оси х, значит, ординаты соответствующих точек <br>прямой отрицательны. A <br>Обратите внимание, что в этом примере мы с <br>помощью графика решили: <br>а) уравнение 2х - 6 = 0 (получили х = 3); <br>б) неравенство 2х - 6 > 0 (получили х > 3); <br>в) неравенство 2я - 6 < 0 (получили х < 3). <br>Замечание. В русском языке часто один и тот же объект <br>называют по-разному, например: «дом», «здание», «со- <br>оружение», «коттедж», «особняк», «барак», «хибара», <br>«избушка». В математическом языке ситуация примерно <br>та же. Скажем, равенство с двумя переменными у = кх + т, <br>где к, т — конкретные числа, можно назвать линейной <br>функцией, можно назвать линейным уравнением с двумя <br>переменными х и у (или с двумя неизвестными х и у), мож- <br>но назвать формулой, можно назвать соотношением, свя- <br>зывающим х и у, можно, наконец, назвать зависимостью <br>между х и у. Это неважно, главное, понимать, что во всех <br>случаях речь идет о математической модели у = кх + т. <br>у, <br>о <br>0 <br>-4 <br>\ <br>\ <br>1 <br>\ <br>\ <br>> <br>б <br>-] <br>*ч <br>,ь <br>рс <br>со <br>5 <br>\ <br>у <br>1? <br>1" <br>0 <br>\ <br>V <br>> <br>1 <br>\ <br>\ <br>\ <br>¦*- <br>ч <br>? <br>X <br>s <br>> <br>1 <br>У <br>\ <br>0 <br>\ <br>N <br>1 <br>\ <br>—ч <br>3 <br>1, <br>ix <br>X <br>у, <br>0 <br>-в <br>/ <br>f <br>1 <br>/ <br>1 <br>it <br>1 <br>1 <br>ч <br>•у <br>У <br>/ <br>^3 <br>»1 <br>/ <br>Рис. 45 <br>Рис. 46 <br>Рис. 47 <br>Рис. 48 <br>120 <br>6 <br>.30. <br>ЛИНЕЙНАЯ <br>ФУНКЦИЯ <br>1 <br>У1 <br>0 <br>t* <br>X <br>\ <br>\ <br>< <br>•*> <br>0 <br>У <br>\ <br>s <br>s <br>* <br>\ <br>X <br>4 <br>6.30. <br>ЛИНЕЙНАЯ ФУНКЦИЯ <br>Рис. 49, a <br>Рис. 49, б <br>возрастание <br>убывание <br>Рассмотрим график линейной функции, изоб- <br>раженный на рисунке 49, а. Если двигаться по это- <br>му графику слева направо, то ординаты точек гра- <br>фика все время увеличиваются, мы как бы «подни- <br>маемся в горку». В таких случаях математики <br>употребляют термин возрастание и говорят так: <br>если k>0, то линейная функция у = kx + m возра- <br>стает. <br>Рассмотрим график линейной функции, изоб- <br>раженный на рисунке 49, б. Если двигаться по этому графику <br>слева направо, то ординаты точек графика все время уменьшают- <br>ся, мы как бы «спускаемся с горки». В таких случаях математи- <br>ки употребляют термин убывание и говорят так: если k < О, то <br>линейная функция у = kx + m убывает. <br>§ 30. ПРЯМАЯ <br><br><br><br><br><br><br>
| + | [[Image:09-06-24.jpg|180px|Таблица]]<br><br>Значения у из второй строки таблицы называют значениями линейной функции у = 2х + 3, соответственно, в точках х = 0, х = 1, х = -1,х=-3. <br> |
| | | | |
| | + | В уравнении (1) переменные хну равноправны, а в уравнении (2) — нет: конкретные значения мы придаем одной из них — переменной х, тогда как значение переменной у зависит от выбранного значения переменной х. Поэтому обычно говорят, что х — независимая переменная (или аргумент), у — зависимая переменная.<br> |
| | | | |
| - | <br>
| + | Обратите внимание: линейная функция - это специальный вид линейного уравнения с двумя переменными. '''[[Линейное уравнение с двумя переменными и его график|Графиком уравнения]]''' у — kx + т, как всякого линейного уравнения с двумя переменными, является прямая — ее называют также графком линейной функции y = kx + тп. Таким образом, справедлива следующая теорема. <br> |
| - | <sub>Школьная библиотека [[Гипермаркет знаний - первый в мире!|онлайн]], учебники и книги по всему предметам, Математика 7 класс [[Математика|скачать]]</sub>
| + | |
| | | | |
| | <br> | | <br> |
| | | | |
| - | '''<u>Содержание урока</u>'''
| + | [[Image:09-06-25.jpg|480px|Теорема 2.]]<br> |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии
| + | |
| - |
| + | |
| - | '''<u>Практика</u>'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
| + | |
| - |
| + | |
| - | '''<u>Иллюстрации</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
| + | |
| - |
| + | |
| - | '''<u>Дополнения</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие
| + | |
| - | '''<u></u>'''
| + | |
| - | <u>Совершенствование учебников и уроков
| + | |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми
| + | |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения
| + | |
| - |
| + | |
| - |
| + | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| | | | |
| | <br> | | <br> |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам]. | + | '''Пример 1.''' Построить график линейной функции у = 2х + 3. <br> |
| | + | |
| | + | Решение. Составим таблицу: <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:09-06-26.jpg|160px|График]]<br><br>Построим на '''[[Ілюстрації до теми Координатна площина|координатной плоскости]]''' хОу точки (0; 3) и (1; 5) и проведем через них прямую. Это и есть график линейной функции у = 2х + 3 (рис. 36).<br> |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:09-06-27.jpg|180px|График линейной функции]]<br> |
| | + | |
| | + | <br>'''''Замечание.''''' В § 25 мы уже говорили о том, как обстоит дело в математике с новыми понятиями, новыми терминами. Часто бывает так: ввели новое понятие, работают с ним, но затем, по мере дальнейшего изучения математики, начинают осознавать, что введенное понятие требует уточнения, развития. Именно так обстояло дело с понятием «тождество». Точно так же обстоит дело и с понятием «функция». Мы еще довольно долго будем привыкать к нему, набираться опыта, работать с этим понятием пока не придем к строгому определению (зто будет в 9 классе). <br> |
| | + | |
| | + | <h2>Практические задания</h2> |
| | + | |
| | + | Многие реальные ситуации описываются '''[[Что такое математическая модель|математическими моделями]]''', представляющими собой линейные функции.Приведем примеры. <br> |
| | + | |
| | + | <u>Первая ситуация.</u> На складе было 500 т угля. Ежедневно стали подвозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней? <br> |
| | + | |
| | + | Если пройдет х дней, то количество у угля на складе (в тоннах) выразится формулой у — 500 + ЗОд:. Таким образом, линейная функция у = З0x + 500 есть математическая модель ситуации. <br> |
| | + | |
| | + | Теперь нетрудно установить, что: <br> |
| | + | |
| | + | при х = 2 имеем у = 560 (в уравнение у = ЗОд: + 500 подставили <br>х = 2 и получили у = 560); <br>при х = 4 имеем у = 620; <br>при х = 10 имеем у = 800. <br> |
| | + | |
| | + | <u>Вторая ситуация.</u> На складе было 500 т угля. Ежедневно стали увозить по 30 т угля. Сколько угля будет на складе через 2, 4,10 дней? <br> |
| | + | |
| | + | Здесь математической моделью ситуации является линейная функция у = 500 - З0x. С помощью этой модели нетрудно ответить на вопрос задачи: <br> |
| | + | |
| | + | если х = 2, то у = 440 (в уравнение у = 500 - З0x подставили <br>х — 2 и получили у = 440); <br>если х = 4, то у = 380; <br>если х = 10, то у = 200. <br> |
| | + | |
| | + | <u>Третья ситуация.</u> Турист проехал на автобусе 15 км от пункта А до Б, а затем продолжил движение из пункта В в том же направлении, но уже пешком, со скоростью 4 км/ч. На каком расстоянии от А будет турист через 2 ч, через 4 ч, через 5 ч ходьбы? <br> |
| | + | |
| | + | Математической моделью ситуации является линейная функция у=15 + 4х, где х — время ходьбы (в часах), у — расстояние от А (в километрах). С помощью этой модели отвечаем на вопрос задачи: <br> |
| | + | |
| | + | если х = 2, то у = 23 (в уравнение у = 15 + 4д: подставили х = 2 <br>и получили у = 23); <br>если д: = 4, то у = 31; <br>если х = 6, то у = 39. <br> |
| | + | |
| | + | На самом деле во всех математических моделях этих трех ситуаций мы допустили неточности, поскольку ничего не сказали о тех ограничениях на х, которые вытекают из смысла задачи. Ведь ясно, что в первой ситуации независимая переменная х может принимать только значения 1, 2, 3, ..., поскольку х — число дней. <br> |
| | + | |
| | + | Следовательно, уточненная математическая модель первой ситуации выглядит так: |
| | + | |
| | + | у = 500 + З0x, где х — '''[[Додавання і віднімання натуральних чисел|натуральное число]]'''. |
| | + | |
| | + | Во второй ситуации независимая переменная х, обозначающая, как и в первой ситуации, число дней, может принимать только значения 1, 2, 3, ..., 16. Действительно, если х = 16, то по формуле у = 500 - З0x находим: у = 500 - 30 • 16 = 20. Значит, уже на 17-й день вывезти со склада 30 т угля не удастся, поскольку на складе к этому дню останется всего 20 т и процесс вывоза угля придется прекратить. Следовательно, уточненная математическая модель второй ситуации выглядит так: |
| | + | |
| | + | у = 500 - ЗОд:, где х = 1, 2, 3, .... 16. |
| | + | |
| | + | В третьей ситуации независимая '''[[Линейное уравнение с двумя переменными и его график|переменная]]''' х теоретически может принять любое неотрицательное значение (напр., значение х = 0, значение х = 2, значение х = 3,5 и т. д.), но практически турист не может шагать с постоянной скоростью без сна и отдыха сколько угодно времени. Значит, нам нужно было сделать разумные ограничения на х, скажем, 0 < х < 6 (т. е. турист идет не более 6 ч). |
| | + | |
| | + | Напомним, что геометрической моделью нестрогого двойного неравенства 0 < х < 6 служит отрезок [0, 6] (рис. 37). Значит, уточненная модель третьей ситуации выглядит так: у = 15 + 4х, где х принадлежит отрезку [0, 6]. |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:09-06-28.jpg|240px|Отрезок]]<br><br>Условимся вместо фразы «х принадлежит множеству X» писать[[Image:09-06-29.jpg|40px|Элемент х принадлежит множеству X]] (читают: «элемент х принадлежит множеству X», е — знак принадлежности). Как видите, наше знакомство с математическим языком постоянно продолжается. |
| | + | |
| | + | Если линейную функцию у = kx + m надо рассматривать не при всех значениях х, а лишь для значений х из некоторого числового промежутка X, то пишут: |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:09-06-30.jpg|180px|Линейная функция]]<br><br>Пример 2. Построить график линейной функции: |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:09-06-31.jpg|360px|График линейной функции]]<br><br>Решение, а) Составим таблицу для линейной функции y = 2x + 1 |
| | + | |
| | + | [[Image:09-06-32.jpg|160px|Таблица]]<br><br>Построим на координатной плоскости хОу точки (-3; 7) и (2; -3) и проведем через них прямую линию. Это — график уравнения у = -2x: + 1. Далее, выделим отрезок, соединяющий построенные точки (рис. 38). Этот отрезок и есть график линейной функции у = -2х+1, гдехе [-3, 2]. |
| | + | |
| | + | Обычно говорят так: мы построили график линейной функции у = - 2х + 1 на отрезке [- 3, 2]. |
| | + | |
| | + | б) Чем отличается этот пример от предыдущего? Линейная функция та же (у = -2х + 1), значит, и ее графиком служит та же прямая. Но — будьте внимательны! — на этот раз х е (-3, 2), т. е. значения х = -3 и х = 2 не рассматриваются, они не принадлежат интервалу (- 3, 2). Как мы отмечали концы интервала на координатной прямой? Светлыми кружочками (рис. 39), об этом мы говорили в § 26. Точно так же и точки (- 3; 7) и B; - 3) придется отметить на чертеже светлыми кружочками. Это будет напоминать нам о том, что берутся лишь те точки прямой у = - 2х + 1, которые лежат между точками, отмеченными кружочками (рис. 40). Впрочем, иногда в таких случаях используют не светлые кружочки, а стрелки (рис. 41). Это непринципиально, главное, понимать, о чем идет речь. |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:09-06-33.jpg|480px|Графики]]<br> |
| | + | |
| | + | <br>'''Пример 3.''' Найти наибольшее и наименьшее значения линейной функции [[Image:09-06-34.jpg|60px|Линейная функция]] на отрезке [0, 6]. <br>Решение. Составим таблицу для линейной функции [[Image:09-06-34.jpg|60px|Линейная функция]]<br> |
| | + | |
| | + | [[Image:09-06-35.jpg|160px|Таблица]]<br><br>Построим на координатной плоскости хОу точки (0; 4) и (6; 7) и проведем через них прямую — график линейной х функции [[Image:09-06-34.jpg|60px|Линейная функция]] (рис. 42). <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:09-06-36.jpg|180px|График линейной функции]] |
| | + | |
| | + | <br>Нам нужно рассмотреть эту линейную функцию не целиком, а на отрезке [0, 6], т. е. для х е [0, 6]. <br> |
| | + | |
| | + | Соответствующий отрезок графика выделен на чертеже. Замечаем, что самая большая ордината у точек, принадлежащих выделенной части, равна 7 — это и есть наибольшее значение линейной функции [[Image:09-06-34.jpg|60px|Линейная функция]] на отрезке [0, 6]. Обычно используют такую запись: у<sub>наиб</sub> =7. |
| | + | |
| | + | Отмечаем, что самая маленькая ордината у точек, принадлежащих выделенной на рисунке 42 части прямой, равна 4 — это и есть наименьшее значение линейной функции[[Image:09-06-34.jpg|60px|Линейная функция]] на отрезке [0, 6]. <br>Обычно используют такую запись: y<sub>наим.</sub> = 4. |
| | + | |
| | + | '''Пример 4.''' Найти у<sub>наиб</sub> и y<sub>наим.</sub> для линейной функции y = -1,5x + 3,5 |
| | + | |
| | + | а) на отрезке [1,5]; б) на интервале (1,5); <br>в) на полуинтервале [1, 5); г) на луче [0, + со); <br>д) на луче (- со, 3]. |
| | + | |
| | + | Решение. Составим таблицу для линейной функции у = -l,5x + 3,5: |
| | + | |
| | + | [[Image:09-06-37.jpg|160px|Таблица]]<br><br>Построим на координатной плоскости хОу точки (1; 2) и (5; - 4) и проведем через них прямую (рис. 43-47). Выделим на построенной прямой часть, соответствующую значениям х из отрезка [1,5] (рис. 43), из интервала A, 5) (рис. 44), из полуинтервала [1, 5) (рис. 45), из луча [0, + со) (рис. 46),из луча(- со, 3] (рис. 47). |
| | + | |
| | + | а) С помощью рисунка 43 нетрудно сделать вывод, что у<sub>наиб</sub> = 2 (этого значения линейная функция достигает при х = 1), а у<sub>наим.</sub> = - 4 (этого значения линейная функция достигает при х = 5). |
| | + | |
| | + | б) Используя рисунок 44, делаем вывод: ни наибольшего, ни наименьшего значений на заданном интервале у данной линейной функции нет. Почему? Дело в том, что, в отличие от предыдущего случая, оба конца отрезка, в которых как раз и достигались наибольшее и наименьшее значения, из рассмотрения исключены. |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:09-06-38.jpg]]<br><br><br>в) С помощью рисунка 45 заключаем, что y<sub>наиб</sub>. = 2 (как и в первом случае), а наименьшего значения у линейной функции нет (как и во втором случае). |
| | + | |
| | + | г) Используя рисунок 46, делаем вывод: у<sub>наиб</sub> = 3,5 (этого значения линейная функция достигает при х = 0), а у<sub>наим</sub>. не существует. |
| | + | |
| | + | д) С помощью рисунка 47 делаем вывод: y<sub>наим</sub> = -1 (этого значения линейная функция достигает при х = 3), а у<sub>наиб</sub>., не существует. |
| | + | |
| | + | Пример 5. Построить график линейной функции |
| | + | |
| | + | у = 2х - 6. С помощью графика ответить на следующие вопросы: |
| | + | |
| | + | ''а) при каком значении х будет у = 0? <br>б) при каких значениях х будет у > 0? <br>в) при каких значениях х будет у < 0? '' |
| | + | |
| | + | Ре ш е ни е. Составим таблицу для линейной функции у = 2х- 6: |
| | + | |
| | + | [[Image:09-06-39.jpg|160px|Таблица]]<br><br>Через точки (0; - 6) и (3; 0) проведем прямую — график функции у = 2х - 6 (рис. 48). |
| | + | |
| | + | а) у = 0 при х = 3. График пересекает ось х в точке х = 3, это и есть точка с ординатой у = 0. <br>б) у > 0 при х > 3. В самом деле если х > 3, то прямая расположена выше оси ж, значит, ординаты соответствующих точек прямой положительны. |
| | + | |
| | + | [[Image:09-06-40.jpg|480px|Линейные графики]] |
| | + | |
| | + | в) у < 0 при х < 3. В самом деле если х < 3, то прямая расположена ниже оси х, значит, ординаты соответствующих точек прямой отрицательны. A |
| | + | |
| | + | Обратите внимание, что в этом примере мы с помощью графика решили: |
| | + | |
| | + | а) уравнение 2х - 6 = 0 (получили х = 3); <br>б) неравенство 2х - 6 > 0 (получили х > 3); <br>в) неравенство 2x - 6 < 0 (получили х < 3). |
| | + | |
| | + | '''''Замечание.''''' В русском языке часто один и тот же объект называют по-разному, например: «дом», «здание», «сооружение», «коттедж», «особняк», «барак», «хибара», «избушка». В математическом языке ситуация примерно та же. Скажем, равенство с двумя переменными у = кх + m, где к, m — конкретные числа, можно назвать линейной функцией, можно назвать линейным уравнением с двумя переменными х и у (или с двумя неизвестными х и у), можно назвать формулой, можно назвать соотношением, связывающим х и у, можно, наконец, назвать зависимостью между х и у. Это неважно, главное, понимать, что во всех случаях речь идет о математической модели у = кх + m |
| | + | |
| | + | [[Image:09-06-41.jpg|480px|Линейные графики]] |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:09-06-42.jpg|480px|Линейные графики]]. |
| | + | |
| | + | <br>Рассмотрим график линейной функции, изображенный на рисунке 49, а. Если двигаться по этому графику слева направо, то ординаты точек графика все время увеличиваются, мы как бы «поднимаемся в горку». В таких случаях математики употребляют термин возрастание и говорят так: если k>0, то линейная функция у = kx + m возрастает. |
| | + | |
| | + | Рассмотрим график линейной функции, изображенный на рисунке 49, б. Если двигаться по этому графику слева направо, то ординаты точек графика все время уменьшаются, мы как бы «спускаемся с горки». В таких случаях математики употребляют термин убывание и говорят так: если k < О, то линейная функция у = kx + m убывает. <br> |
| | + | |
| | + | <h2>Линейная функция в жизни</h2> |
| | + | |
| | + | А теперь давайте подведем итог этой темы. Мы с вами уже познакомились с таким понятие, как линейная функция, знаем ее свойства и научились строить графики. Так же, вы рассматривали частные случаи линейной функции и узнали от чего зависит взаимное расположение графиков линейных функций. Но, оказывается, в нашей повседневной жизни мы также постоянно пересекаемся с этой математической моделью. |
| | + | |
| | + | Давайте мы с вами подумаем, какие реальные жизненные ситуации связаны с таким понятием, как линейные функции? А также, между какими величинами или жизненными ситуациями, возможно, устанавливать линейную зависимость? |
| | + | |
| | + | Многие из вас, наверное, не совсем представляют, зачем им нужно изучать линейные функции, ведь это вряд ли пригодится в дальнейшей жизни. Но здесь вы глубоко ошибаетесь, потому что с функциями мы сталкиваемся постоянно и повсюду. Так как, даже обычная ежемесячная квартплата также является функцией, которая зависит от многих переменных. А к этим переменным относится метраж площади, количество жильцов, тарифов, использование электроэнергии и т.д. |
| | + | |
| | + | Конечно же, самыми распространенными примерами функций линейной зависимости, с которыми мы с вами сталкивались – это уроки математики. |
| | + | |
| | + | Мы с вами решали задачи, где находили расстояния, которые проезжали машины, поезда или проходили пешеходы при определенной скорости движения. Это и есть линейные функции времени движения. Но ведь эти примеры применимы не только в математике, они присутствуют в нашей повседневной жизни. |
| | + | |
| | + | Калорийности молочных продуктов зависит жирности, а такая зависимость, как правило, является линейной функцией. Так, например, при увеличении сметане процента жирности, увеличивается и калорийность продукта. |
| | + | |
| | + | <br> |
| | + | [[Image:7kl_LinFunk01.jpg|700x700px|ЛФ]] |
| | + | <br> |
| | + | |
| | + | Теперь давайте сделаем подсчеты и найдем значения k и b, решив систему уравнений: |
| | + | |
| | + | <br> |
| | + | [[Image:7kl_LinFunk02.jpg|300x300px|ЛФ]] |
| | + | <br> |
| | + | |
| | + | Теперь давайте выведем формулу зависимости: |
| | + | |
| | + | y = 8,7x + 30 |
| | + | |
| | + | В итоге мы получили линейную зависимость. |
| | + | |
| | + | Чтобы знать скорость распространения звука в зависимости от температуры, возможно, узнать, применив формулу: v = 331 +0,6t, где v - скорость (в м/с), t - температура. Если мы начертим график этой зависимости, то увидим, что он будет линейным, то есть представлять прямую линию. |
| | + | |
| | + | И таких практических использований знаний в применении линейной функциональной зависимости можно перечислять долго. Начиная от платы за телефон, длины и роста волос и даже пословиц в литературе. И этот список можно продолжать до бесконечности. |
| | + | |
| | + | <br> <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| | + | |
| | + | <br> |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
Текущая версия на 09:19, 17 августа 2015
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Линейная функция и ее график
Линейная функция и ее график
Алгоритм построения графика уравнения ах + by + с = 0, который мы сформулировали в § 28, при всей его четкости и определенности математикам не очень нравится. Обычно они выдвигают претензии к первым двум шагам алгоритма. Зачем, говорят они, дважды решать уравнение относительно переменной у: сначала ах1 + Ьу + с = О, затем ахг + Ьу + с = О? Не лучше ли сразу выразить у из уравнения ах + by + с = 0, тогда легче будет проводить вычисления (и, главное, быстрее)? Давайте проверим. Рассмотрим сначала уравнение 3x - 2у + 6 = 0 (см. пример 2 из § 28).
Имеем:
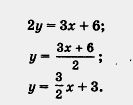
Придавая х конкретные значения, легко вычислить соответствующие значения у. Например, при х = 0 получаем у = 3; при х = -2 имеем у = 0; при х = 2 имеем у = 6; при х = 4 получаем: у = 9.
Видите, как легко и быстро найдены точки (0; 3), (- 2; 0), (2; 6) и (4; 9), которые были выделены в примере 2 из § 28.
Точно так же уравнение Ьх - 2у = 0 (см. пример 4 из § 28) можно было преобразовать к виду 2у =16 -3x . далее у = 2,5x; нетрудно найти точки (0; 0) и (2; 5), удовлетворяющие этому уравнению.
Наконец, уравнение 3x + 2у - 16 = 0 из того же примера можно преобразовать к виду 2y = 16 -3x и далее 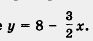 нетрудно найти точки (0; 0) и (2; 5), которые ему удовлетворяют. нетрудно найти точки (0; 0) и (2; 5), которые ему удовлетворяют.
Рассмотрим теперь указанные преобразования в общем виде.
Имеем:
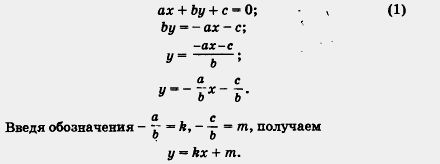
Таким образом, линейное уравнение (1) с двумя переменными х и у всегда можно преобразовать к виду
y = kx + m,(2) где k,m — числа (коэффициенты), причем 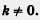 . .
Этот частный вид линейного уравнения будем называть линейной функцией.
С помощью равенства (2) легко, указав конкретное значение х, вычислить соответствующее значение у. Пусть, например,
у = 2х + 3. Тогда:
если х = 0, то у = 3;
если х = 1, то у = 5;
если х = -1, то у = 1;
если х = 3, то у = 9 и т. д.
Обычно эти результаты оформляют в виде таблицы:
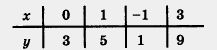
Значения у из второй строки таблицы называют значениями линейной функции у = 2х + 3, соответственно, в точках х = 0, х = 1, х = -1,х=-3.
В уравнении (1) переменные хну равноправны, а в уравнении (2) — нет: конкретные значения мы придаем одной из них — переменной х, тогда как значение переменной у зависит от выбранного значения переменной х. Поэтому обычно говорят, что х — независимая переменная (или аргумент), у — зависимая переменная.
Обратите внимание: линейная функция - это специальный вид линейного уравнения с двумя переменными. Графиком уравнения у — kx + т, как всякого линейного уравнения с двумя переменными, является прямая — ее называют также графком линейной функции y = kx + тп. Таким образом, справедлива следующая теорема.
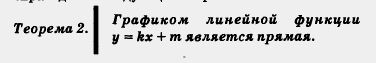
Пример 1. Построить график линейной функции у = 2х + 3.
Решение. Составим таблицу:
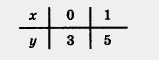
Построим на координатной плоскости хОу точки (0; 3) и (1; 5) и проведем через них прямую. Это и есть график линейной функции у = 2х + 3 (рис. 36).
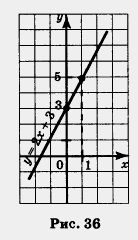
Замечание. В § 25 мы уже говорили о том, как обстоит дело в математике с новыми понятиями, новыми терминами. Часто бывает так: ввели новое понятие, работают с ним, но затем, по мере дальнейшего изучения математики, начинают осознавать, что введенное понятие требует уточнения, развития. Именно так обстояло дело с понятием «тождество». Точно так же обстоит дело и с понятием «функция». Мы еще довольно долго будем привыкать к нему, набираться опыта, работать с этим понятием пока не придем к строгому определению (зто будет в 9 классе).
Практические задания
Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции.Приведем примеры.
Первая ситуация. На складе было 500 т угля. Ежедневно стали подвозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней?
Если пройдет х дней, то количество у угля на складе (в тоннах) выразится формулой у — 500 + ЗОд:. Таким образом, линейная функция у = З0x + 500 есть математическая модель ситуации.
Теперь нетрудно установить, что:
при х = 2 имеем у = 560 (в уравнение у = ЗОд: + 500 подставили
х = 2 и получили у = 560);
при х = 4 имеем у = 620;
при х = 10 имеем у = 800.
Вторая ситуация. На складе было 500 т угля. Ежедневно стали увозить по 30 т угля. Сколько угля будет на складе через 2, 4,10 дней?
Здесь математической моделью ситуации является линейная функция у = 500 - З0x. С помощью этой модели нетрудно ответить на вопрос задачи:
если х = 2, то у = 440 (в уравнение у = 500 - З0x подставили
х — 2 и получили у = 440);
если х = 4, то у = 380;
если х = 10, то у = 200.
Третья ситуация. Турист проехал на автобусе 15 км от пункта А до Б, а затем продолжил движение из пункта В в том же направлении, но уже пешком, со скоростью 4 км/ч. На каком расстоянии от А будет турист через 2 ч, через 4 ч, через 5 ч ходьбы?
Математической моделью ситуации является линейная функция у=15 + 4х, где х — время ходьбы (в часах), у — расстояние от А (в километрах). С помощью этой модели отвечаем на вопрос задачи:
если х = 2, то у = 23 (в уравнение у = 15 + 4д: подставили х = 2
и получили у = 23);
если д: = 4, то у = 31;
если х = 6, то у = 39.
На самом деле во всех математических моделях этих трех ситуаций мы допустили неточности, поскольку ничего не сказали о тех ограничениях на х, которые вытекают из смысла задачи. Ведь ясно, что в первой ситуации независимая переменная х может принимать только значения 1, 2, 3, ..., поскольку х — число дней.
Следовательно, уточненная математическая модель первой ситуации выглядит так:
у = 500 + З0x, где х — натуральное число.
Во второй ситуации независимая переменная х, обозначающая, как и в первой ситуации, число дней, может принимать только значения 1, 2, 3, ..., 16. Действительно, если х = 16, то по формуле у = 500 - З0x находим: у = 500 - 30 • 16 = 20. Значит, уже на 17-й день вывезти со склада 30 т угля не удастся, поскольку на складе к этому дню останется всего 20 т и процесс вывоза угля придется прекратить. Следовательно, уточненная математическая модель второй ситуации выглядит так:
у = 500 - ЗОд:, где х = 1, 2, 3, .... 16.
В третьей ситуации независимая переменная х теоретически может принять любое неотрицательное значение (напр., значение х = 0, значение х = 2, значение х = 3,5 и т. д.), но практически турист не может шагать с постоянной скоростью без сна и отдыха сколько угодно времени. Значит, нам нужно было сделать разумные ограничения на х, скажем, 0 < х < 6 (т. е. турист идет не более 6 ч).
Напомним, что геометрической моделью нестрогого двойного неравенства 0 < х < 6 служит отрезок [0, 6] (рис. 37). Значит, уточненная модель третьей ситуации выглядит так: у = 15 + 4х, где х принадлежит отрезку [0, 6].
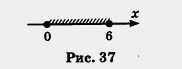
Условимся вместо фразы «х принадлежит множеству X» писать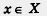 (читают: «элемент х принадлежит множеству X», е — знак принадлежности). Как видите, наше знакомство с математическим языком постоянно продолжается. (читают: «элемент х принадлежит множеству X», е — знак принадлежности). Как видите, наше знакомство с математическим языком постоянно продолжается.
Если линейную функцию у = kx + m надо рассматривать не при всех значениях х, а лишь для значений х из некоторого числового промежутка X, то пишут:
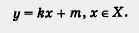
Пример 2. Построить график линейной функции:

Решение, а) Составим таблицу для линейной функции y = 2x + 1
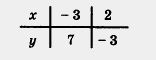
Построим на координатной плоскости хОу точки (-3; 7) и (2; -3) и проведем через них прямую линию. Это — график уравнения у = -2x: + 1. Далее, выделим отрезок, соединяющий построенные точки (рис. 38). Этот отрезок и есть график линейной функции у = -2х+1, гдехе [-3, 2].
Обычно говорят так: мы построили график линейной функции у = - 2х + 1 на отрезке [- 3, 2].
б) Чем отличается этот пример от предыдущего? Линейная функция та же (у = -2х + 1), значит, и ее графиком служит та же прямая. Но — будьте внимательны! — на этот раз х е (-3, 2), т. е. значения х = -3 и х = 2 не рассматриваются, они не принадлежат интервалу (- 3, 2). Как мы отмечали концы интервала на координатной прямой? Светлыми кружочками (рис. 39), об этом мы говорили в § 26. Точно так же и точки (- 3; 7) и B; - 3) придется отметить на чертеже светлыми кружочками. Это будет напоминать нам о том, что берутся лишь те точки прямой у = - 2х + 1, которые лежат между точками, отмеченными кружочками (рис. 40). Впрочем, иногда в таких случаях используют не светлые кружочки, а стрелки (рис. 41). Это непринципиально, главное, понимать, о чем идет речь.
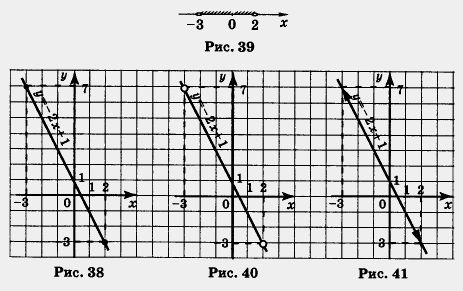
Пример 3. Найти наибольшее и наименьшее значения линейной функции 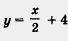 на отрезке [0, 6]. на отрезке [0, 6].
Решение. Составим таблицу для линейной функции 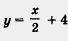
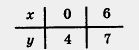
Построим на координатной плоскости хОу точки (0; 4) и (6; 7) и проведем через них прямую — график линейной х функции 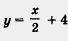 (рис. 42). (рис. 42).
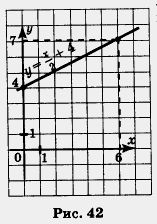
Нам нужно рассмотреть эту линейную функцию не целиком, а на отрезке [0, 6], т. е. для х е [0, 6].
Соответствующий отрезок графика выделен на чертеже. Замечаем, что самая большая ордината у точек, принадлежащих выделенной части, равна 7 — это и есть наибольшее значение линейной функции 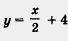 на отрезке [0, 6]. Обычно используют такую запись: унаиб =7. на отрезке [0, 6]. Обычно используют такую запись: унаиб =7.
Отмечаем, что самая маленькая ордината у точек, принадлежащих выделенной на рисунке 42 части прямой, равна 4 — это и есть наименьшее значение линейной функции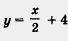 на отрезке [0, 6]. на отрезке [0, 6].
Обычно используют такую запись: yнаим. = 4.
Пример 4. Найти унаиб и yнаим. для линейной функции y = -1,5x + 3,5
а) на отрезке [1,5]; б) на интервале (1,5);
в) на полуинтервале [1, 5); г) на луче [0, + со);
д) на луче (- со, 3].
Решение. Составим таблицу для линейной функции у = -l,5x + 3,5:
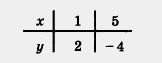
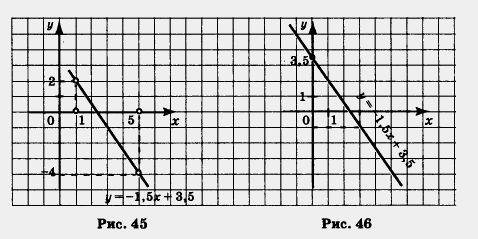
Построим на координатной плоскости хОу точки (1; 2) и (5; - 4) и проведем через них прямую (рис. 43-47). Выделим на построенной прямой часть, соответствующую значениям х из отрезка [1,5] (рис. 43), из интервала A, 5) (рис. 44), из полуинтервала [1, 5) (рис. 45), из луча [0, + со) (рис. 46),из луча(- со, 3] (рис. 47).
а) С помощью рисунка 43 нетрудно сделать вывод, что унаиб = 2 (этого значения линейная функция достигает при х = 1), а унаим. = - 4 (этого значения линейная функция достигает при х = 5).
б) Используя рисунок 44, делаем вывод: ни наибольшего, ни наименьшего значений на заданном интервале у данной линейной функции нет. Почему? Дело в том, что, в отличие от предыдущего случая, оба конца отрезка, в которых как раз и достигались наибольшее и наименьшее значения, из рассмотрения исключены.
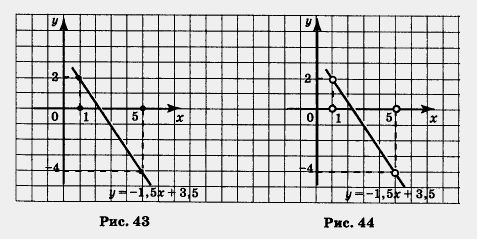
в) С помощью рисунка 45 заключаем, что yнаиб. = 2 (как и в первом случае), а наименьшего значения у линейной функции нет (как и во втором случае).
г) Используя рисунок 46, делаем вывод: унаиб = 3,5 (этого значения линейная функция достигает при х = 0), а унаим. не существует.
д) С помощью рисунка 47 делаем вывод: yнаим = -1 (этого значения линейная функция достигает при х = 3), а унаиб., не существует.
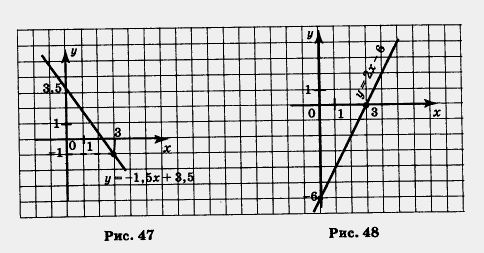
Пример 5. Построить график линейной функции
у = 2х - 6. С помощью графика ответить на следующие вопросы:
а) при каком значении х будет у = 0?
б) при каких значениях х будет у > 0?
в) при каких значениях х будет у < 0?
Ре ш е ни е. Составим таблицу для линейной функции у = 2х- 6:
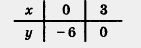
Через точки (0; - 6) и (3; 0) проведем прямую — график функции у = 2х - 6 (рис. 48).
а) у = 0 при х = 3. График пересекает ось х в точке х = 3, это и есть точка с ординатой у = 0.
б) у > 0 при х > 3. В самом деле если х > 3, то прямая расположена выше оси ж, значит, ординаты соответствующих точек прямой положительны.
в) у < 0 при х < 3. В самом деле если х < 3, то прямая расположена ниже оси х, значит, ординаты соответствующих точек прямой отрицательны. A
Обратите внимание, что в этом примере мы с помощью графика решили:
а) уравнение 2х - 6 = 0 (получили х = 3);
б) неравенство 2х - 6 > 0 (получили х > 3);
в) неравенство 2x - 6 < 0 (получили х < 3).
Замечание. В русском языке часто один и тот же объект называют по-разному, например: «дом», «здание», «сооружение», «коттедж», «особняк», «барак», «хибара», «избушка». В математическом языке ситуация примерно та же. Скажем, равенство с двумя переменными у = кх + m, где к, m — конкретные числа, можно назвать линейной функцией, можно назвать линейным уравнением с двумя переменными х и у (или с двумя неизвестными х и у), можно назвать формулой, можно назвать соотношением, связывающим х и у, можно, наконец, назвать зависимостью между х и у. Это неважно, главное, понимать, что во всех случаях речь идет о математической модели у = кх + m
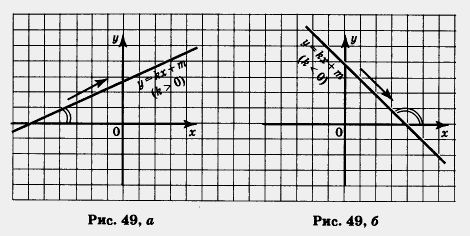 . .
Рассмотрим график линейной функции, изображенный на рисунке 49, а. Если двигаться по этому графику слева направо, то ординаты точек графика все время увеличиваются, мы как бы «поднимаемся в горку». В таких случаях математики употребляют термин возрастание и говорят так: если k>0, то линейная функция у = kx + m возрастает.
Рассмотрим график линейной функции, изображенный на рисунке 49, б. Если двигаться по этому графику слева направо, то ординаты точек графика все время уменьшаются, мы как бы «спускаемся с горки». В таких случаях математики употребляют термин убывание и говорят так: если k < О, то линейная функция у = kx + m убывает.
Линейная функция в жизни
А теперь давайте подведем итог этой темы. Мы с вами уже познакомились с таким понятие, как линейная функция, знаем ее свойства и научились строить графики. Так же, вы рассматривали частные случаи линейной функции и узнали от чего зависит взаимное расположение графиков линейных функций. Но, оказывается, в нашей повседневной жизни мы также постоянно пересекаемся с этой математической моделью.
Давайте мы с вами подумаем, какие реальные жизненные ситуации связаны с таким понятием, как линейные функции? А также, между какими величинами или жизненными ситуациями, возможно, устанавливать линейную зависимость?
Многие из вас, наверное, не совсем представляют, зачем им нужно изучать линейные функции, ведь это вряд ли пригодится в дальнейшей жизни. Но здесь вы глубоко ошибаетесь, потому что с функциями мы сталкиваемся постоянно и повсюду. Так как, даже обычная ежемесячная квартплата также является функцией, которая зависит от многих переменных. А к этим переменным относится метраж площади, количество жильцов, тарифов, использование электроэнергии и т.д.
Конечно же, самыми распространенными примерами функций линейной зависимости, с которыми мы с вами сталкивались – это уроки математики.
Мы с вами решали задачи, где находили расстояния, которые проезжали машины, поезда или проходили пешеходы при определенной скорости движения. Это и есть линейные функции времени движения. Но ведь эти примеры применимы не только в математике, они присутствуют в нашей повседневной жизни.
Калорийности молочных продуктов зависит жирности, а такая зависимость, как правило, является линейной функцией. Так, например, при увеличении сметане процента жирности, увеличивается и калорийность продукта.
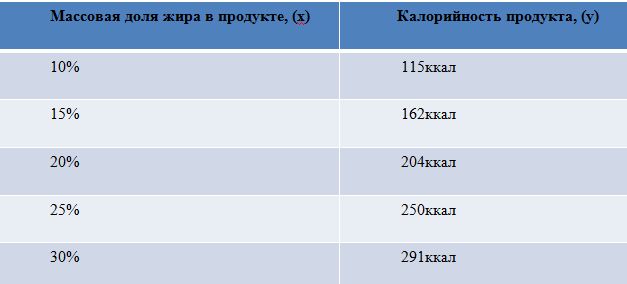
Теперь давайте сделаем подсчеты и найдем значения k и b, решив систему уравнений:
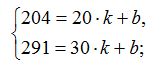
Теперь давайте выведем формулу зависимости:
y = 8,7x + 30
В итоге мы получили линейную зависимость.
Чтобы знать скорость распространения звука в зависимости от температуры, возможно, узнать, применив формулу: v = 331 +0,6t, где v - скорость (в м/с), t - температура. Если мы начертим график этой зависимости, то увидим, что он будет линейным, то есть представлять прямую линию.
И таких практических использований знаний в применении линейной функциональной зависимости можно перечислять долго. Начиная от платы за телефон, длины и роста волос и даже пословиц в литературе. И этот список можно продолжать до бесконечности.
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
|