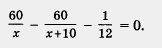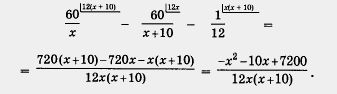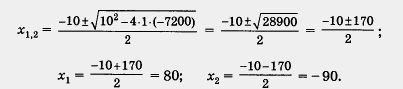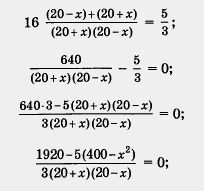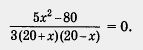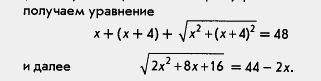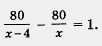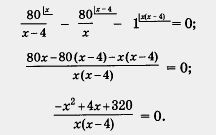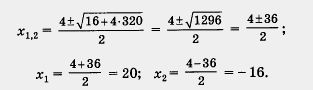|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Рациональные уравнения как математические модели реальных ситуаций</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Рациональные уравнения как математические модели реальных ситуаций, рациональные уравнения, математической модели, дроби, отрицательным числом, задачи, математический язык, преобразования, треугольника, теореме, корни, двузначное число, цифры, формулу</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Рациональные уравнения как математические модели реальных ситуаций''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Рациональные уравнения как математические модели реальных ситуаций''' |
| Строка 5: |
Строка 5: |
| | '''Рациональные уравнения как математические модели реальных ситуаций'''<br> | | '''Рациональные уравнения как математические модели реальных ситуаций'''<br> |
| | | | |
| - | <br>То, что рациональные уравнения могут служить математическими моделями реальных ситуаций, вам известно, целый ряд соответствующих примеров мы рассмотрели выше в § 7 и ранее, в учебнике «Алгебра-7». Сейчас поговорим об этом более подробно. <br> | + | <br>То, что '''[[Рациональные уравнения|рациональные уравнения]]''' могут служить математическими моделями реальных ситуаций, вам известно, целый ряд соответствующих примеров мы рассмотрели выше в § 7 и ранее, в учебнике «Алгебра-7». Сейчас поговорим об этом более подробно. <br> |
| | | | |
| - | '''Пример 1.''' Перегон в 60 км поезд должен был проехать с постоянной скоростью за определенное расписанием время. Простояв у семафора перед перегоном 5 мин, машинист вынужден был увеличить скорость прохождения перегона на 10 км/ч, чтобы наверстать к окончанию прохождения перегона <br>потерянные 5 мин. С какой скоростью поезд должен был пройти перегон по расписанию? <br>Решение. <br><u>'''Первый этап.'''</u> Составление математической модели. Пусть х км/ч — скорость поезда по расписанию. Так как протяженность перегона равна 60 км, то время, отведенное расписанием на прохождение перегона, составляет [[Image:14-06-1.jpg]] ч. <br> | + | '''Пример 1.''' Перегон в 60 км поезд должен был проехать с постоянной скоростью за определенное расписанием время. Простояв у семафора перед перегоном 5 мин, машинист вынужден был увеличить скорость прохождения перегона на 10 км/ч, чтобы наверстать к окончанию прохождения перегона потерянные 5 мин. С какой скоростью поезд должен был пройти перегон по расписанию? <br> |
| | | | |
| - | Фактически поезд прошел перегон в 60 км со скоростью (х + 10) км/ч, значит, время, затраченное на прохождение перегона, равно [[Image:14-06-2.jpg]] ч. <br>Из двух величин — [[Image:14-06-1.jpg]]ч и [[Image:14-06-2.jpg]] ч первая больше второй на 5 мин, т. е. на [[Image:14-06-3.jpg]] ч. Значит, мы приходим к уравнению <br>[[Image:14-06-4.jpg]]<br>Математическая модель задачи составлена. Это — рациональное уравнение. <br> | + | Решение. <br> |
| | + | |
| | + | <u>'''Первый этап.'''</u> Составление '''[[Что такое математическая модель|математической модели]]'''. Пусть х км/ч — скорость поезда по расписанию. Так как протяженность перегона равна 60 км, то время, отведенное расписанием на прохождение перегона, составляет [[Image:14-06-1.jpg]] ч. <br> |
| | + | |
| | + | Фактически поезд прошел перегон в 60 км со скоростью (х + 10) км/ч, значит, время, затраченное на прохождение перегона, равно [[Image:14-06-2.jpg|Дробь]] ч. <br>Из двух величин — [[Image:14-06-1.jpg]]ч и [[Image:14-06-2.jpg|Дробь]] ч первая больше второй на 5 мин, т. е. на [[Image:14-06-3.jpg]] ч. Значит, мы приходим к уравнению <br>[[Image:14-06-4.jpg|120px|Уравнение]]<br>Математическая модель задачи составлена. Это — рациональное уравнение. <br> |
| | | | |
| | <u>'''Второй этап.'''</u> Работа с составленной моделью. <br>Имеем <br> | | <u>'''Второй этап.'''</u> Работа с составленной моделью. <br>Имеем <br> |
| | | | |
| - | [[Image:14-06-5.jpg]]<br><br>Преобразуем левую часть уравнения <br> | + | [[Image:14-06-5.jpg|180px|Уравнение]]<br><br>Преобразуем левую часть уравнения <br> |
| | | | |
| - | [[Image:14-06-6.jpg]]<br><br>Приравняв числитель этой дроби нулю, получим квадратное уравнение - х<sup>2</sup> - 10х + 7200 = 0 или, переходя к более удобной записи, х<sup>2</sup> + 10х - 7200 = 0. <br>Применяя известную формулу, находим <br> | + | [[Image:14-06-6.jpg|320px|Уравнение]]<br><br>Приравняв числитель этой '''[[Задачі до уроку «Додавання і віднімання звичайних дробів з однаковими знаменниками.»|дроби]]''' нулю, получим квадратное уравнение - х<sup>2</sup> - 10х + 7200 = 0 или, переходя к более удобной записи, х<sup>2</sup> + 10х - 7200 = 0. <br> |
| | | | |
| - | [[Image:14-06-7.jpg]]<br><br>Оба значения удовлетворяют условию [[Image:14-06-8.jpg]], следовательно, эти значения — корни составленного рационального уравнения. <u>'''<br>Третий этап.'''</u> Ответ на вопрос задачи. <br>Спрашивается, с какой скоростью поезд должен был пройти перегон по расписанию? Именно эту величину мы обозначили значение нас явно не устраивает, поскольку скорость движения поезда не может выражаться отрицательным числом. Значит, выбираем значение х = 80, это и есть ответ на вопрос задачи.<br>
| + | Применяя известную формулу, находим <br> |
| | | | |
| - | О т в е т: 80 км/ч. <br>Сделаем некоторые комментарии к выполненному решению. <br>1. Конечно, рассмотренная ситуация несколько идеализирована: вряд ли в реальной жизни поезд пройдет весь перегон с постоянной скоростью, ведь всегда есть и ускорения, и замедления. Но на такую идеализацию математикам приходится идти сознательно. <br>
| + | [[Image:14-06-7.jpg|480px|Уравнение]]<br><br>Оба значения удовлетворяют условию [[Image:14-06-8.jpg|120px|Условие]], следовательно, эти значения — корни составленного рационального уравнения. <u</u><br> |
| | | | |
| - | 2. В очередной раз обращаем ваше внимание на то, что мы воспользовались привычной схемой рассуждений: составление математической модели, работа с составленной моделью, ответ на вопрос задачи.
| + | <u>'''<br>Третий этап.'''</u> Ответ на вопрос задачи. <br> |
| | | | |
| - | 3. Подчеркнем, что первый этап, т. е. составk ление математической модели, — ключевой в решении задачи. На этом этапе осуществляется перевод условия задачи с обыденного языка на математический язык, т. е. выполняется серьезная творческая работа. Серьезная работа проводится и на втором этапе, но эта работа не творческая, а чисто техническая, поскольку, действуя по алгоритму, особенно думать не приходится.
| + | Спрашивается, с какой скоростью поезд должен был пройти перегон по расписанию? Именно эту величину мы обозначили значение нас явно не устраивает, поскольку скорость движения поезда не может выражаться '''[[Презентація уроку на тему «Додатні та від'ємні числа. Число 0»|отрицательным числом]]'''. Значит, выбираем значение х = 80, это и есть ответ на вопрос задачи.<br> |
| | | | |
| - | Вернемся к рассмотренной задаче и проанализируем, как осуществляется перевод с обыденного языка на математический. <br>Искомую величину мы обозначили буквой х. Это дало нам возможность оперировать с искомой скоростью, ведь с точки зрения алгебры не важно, имеем ли мы дело с числами или с буквами.
| + | О т в е т: 80 км/ч. <br> |
| | | | |
| - | Зная путь 60 км) и скорость (х км/ч) и использовав физический закон равномерного движения s = vt (s — путь, v — скорость, t — время), мы нашли время, предусмотренное расписанием, — оно выражается дробью [[Image:14-06-1.jpg]] ч. <br>По условию, перегон был пройден со скоростью, на 10 км/ч большей, чем предполагалось расписанием. Перевод этого условия на математический язык дал следующее: (х + 10) км/ч — фактическая скорость прохождения перегона, а [[Image:14-06-2.jpg]] ч — фактическое время движения поезда по перегону в 60 км. <br>Далее, согласно условию, на рассматриваемом перегоне поезд выиграл, по сравнению с расписанием, 5 мин, т. е. [[Image:14-06-3.jpg]] ч. <br>Иными словами, время, предусмотренное расписанием ([[Image:14-06-1.jpg]] ч ), больше фактического времени [[Image:14-06-2.jpg]] ч ) на [[Image:14-06-3.jpg]] ч. <br>На математическом языке это означает, что [[Image:14-06-4.jpg]] (из большей величины вычли меньшую и получили указанную в условии разность). <br> | + | Сделаем некоторые комментарии к выполненному решению. <br> |
| | + | |
| | + | 1. Конечно, рассмотренная ситуация несколько идеализирована: вряд ли в реальной жизни поезд пройдет весь перегон с постоянной скоростью, ведь всегда есть и ускорения, и замедления. Но на такую идеализацию математикам приходится идти сознательно. <br> |
| | + | |
| | + | 2. В очередной раз обращаем ваше внимание на то, что мы воспользовались привычной схемой рассуждений: составление математической модели, работа с составленной моделью, ответ на вопрос '''[[Задачі до теми Розв'язування задач за допомогою рівнянь|задачи]]'''. |
| | + | |
| | + | 3. Подчеркнем, что первый этап, т. е. составление математической модели, — ключевой в решении задачи. На этом этапе осуществляется перевод условия задачи с обыденного языка на '''[[Что такое математический язык|математический язык]]''', т. е. выполняется серьезная творческая работа. Серьезная работа проводится и на втором этапе, но эта работа не творческая, а чисто техническая, поскольку, действуя по алгоритму, особенно думать не приходится. |
| | + | |
| | + | Вернемся к рассмотренной задаче и проанализируем, как осуществляется перевод с обыденного языка на математический. <br> |
| | + | |
| | + | Искомую величину мы обозначили буквой х. Это дало нам возможность оперировать с искомой скоростью, ведь с точки зрения алгебры не важно, имеем ли мы дело с числами или с буквами. |
| | + | |
| | + | Зная путь 60 км) и скорость (х км/ч) и использовав физический закон равномерного движения s = vt (s — путь, v — скорость, t — время), мы нашли время, предусмотренное расписанием, — оно выражается дробью [[Image:14-06-1.jpg]] ч. <br>По условию, перегон был пройден со скоростью, на 10 км/ч большей, чем предполагалось расписанием. Перевод этого условия на математический язык дал следующее: (х + 10) км/ч — фактическая скорость прохождения перегона, а [[Image:14-06-2.jpg|Дробь]] ч — фактическое время движения поезда по перегону в 60 км. <br>Далее, согласно условию, на рассматриваемом перегоне поезд выиграл, по сравнению с расписанием, 5 мин, т. е. [[Image:14-06-3.jpg]] ч. <br>Иными словами, время, предусмотренное расписанием ([[Image:14-06-1.jpg]] ч ), больше фактического времени [[Image:14-06-2.jpg|Дробь]] ч ) на [[Image:14-06-3.jpg]] ч. <br>На математическом языке это означает, что [[Image:14-06-4.jpg|120px|Уравнение]] (из большей величины вычли меньшую и получили указанную в условии разность). <br> |
| | | | |
| | Обратите внимание на то, что сравнивать надо величины одного и того же наименования (в данном уравнении это — часы). <br> | | Обратите внимание на то, что сравнивать надо величины одного и того же наименования (в данном уравнении это — часы). <br> |
| | | | |
| - | '''Пример 2.''' Пристани А и В расположены на реке, причем В — на 80 км ниже по течению, чем А. Катер прошел путь из А в В и обратно за 8 ч 20 мин. За какое время катер прошел расстояние от А до В и расстояние от В до А, если известно, что его собственная скорость (скорость в стоячей воде) равна 20 км/ч? <br>Решение. <br><u>'''Первый этап'''</u>. Составление математической модели. <br>Пусть х км/ч — скорость течения реки. Тогда: <br>(20 + х) км/ч — скорость движения катера по течению; <br>(20 - х) км/ч — скорость движения катера против течения; [[Image:14-06-9.jpg]] — время движения катера по течению; <br>[[Image:14-06-10.jpg]] время движения катера против течения. <br>По условию, на путь туда и обратно катер затратил 8 ч 20 мин, т. е. [[Image:14-06-11.jpg]] Но время, затраченное катером на путь из А в В и обратно, выражается суммой дробей [[Image:14-06-12.jpg]]<br>Значит, мы приходим к уравнению <br> | + | '''Пример 2.''' Пристани А и В расположены на реке, причем В — на 80 км ниже по течению, чем А. Катер прошел путь из А в В и обратно за 8 ч 20 мин. За какое время катер прошел расстояние от А до В и расстояние от В до А, если известно, что его собственная скорость (скорость в стоячей воде) равна 20 км/ч? <br> |
| | | | |
| - | [[Image:14-06-13.jpg]]<br><br>Перевод условий задачи с обыденного языка на математический состоялся, математическая модель составлена. Это — рациональное уравнение. <br> | + | Решение. <br> |
| | + | |
| | + | <br><u>'''Первый этап'''</u>. Составление математической модели. <br> |
| | + | |
| | + | Пусть х км/ч — скорость течения реки. Тогда: (20 + х) км/ч — скорость движения катера по течению; <br>(20 - х) км/ч — скорость движения катера против течения; [[Image:14-06-9.jpg|Дробь]] — время движения катера по течению; <br>[[Image:14-06-10.jpg|Дробь]] время движения катера против течения. <br>По условию, на путь туда и обратно катер затратил 8 ч 20 мин, т. е. [[Image:14-06-11.jpg|Дробь]] Но время, затраченное катером на путь из А в В и обратно, выражается суммой дробей [[Image:14-06-12.jpg|120px|Сумма дробей]]<br>Значит, мы приходим к '''[[Тестові завдання до уроку на тему «Рівняння зі змінною в знаменнику»|уравнению]]''' <br> |
| | + | |
| | + | [[Image:14-06-13.jpg|180px|Уравнение]]<br><br>Перевод условий задачи с обыденного языка на математический состоялся, математическая модель составлена. Это — рациональное уравнение. <br> |
| | | | |
| | <u>'''Второй этап.'''</u> Работа с составленной моделью. <br>Имеем <br> | | <u>'''Второй этап.'''</u> Работа с составленной моделью. <br>Имеем <br> |
| | | | |
| - | [[Image:14-06-14.jpg]]<br><br>Есть смысл разделить обе части уравнения на 5, хотя бы для того, чтобы облегчить последующие вычисления: <br> | + | [[Image:14-06-14.jpg|180px|Уравнение]]<br><br>Есть смысл разделить обе части уравнения на 5, хотя бы для того, чтобы облегчить последующие вычисления: <br> |
| | + | |
| | + | [[Image:14-06-15.jpg|180px|Уравнение]]<br><br>Выполним дальнейшие '''[[Преобразование тригонометрических выражений. Основные результаты|преобразования]]''': <br> |
| | + | |
| | + | [[Image:14-06-16.jpg|240px|Уравнение]]<br>[[Image:14-06-17.jpg|160px|Уравнение]]<br> |
| | + | |
| | + | Из уравнения 5х<sup>2</sup> - 80 = 0 находим х<sup>2</sup> = 16, х<sub>1,2</sub> = ± 4. <br>Оба эти значения удовлетворяют условию [[Image:14-06-18.jpg|Уравнение]], значит, они являются корнями составленного рационального уравнения. <br> |
| | + | |
| | + | <br><u>'''Третий этап.'''</u> Ответ на вопрос задачи. <br> |
| | + | |
| | + | <u>Во-первых</u>, за х мы приняли скорость течения реки, а отрицательным числом скорость выражаться не может. Значит, из двух значений 4 и - 4 выбираем первое и отбрасываем второе. <br> |
| | + | |
| | + | <u>Во-вторых</u>, нас не спрашивают, чему равна скорость течения реки, а спрашивают, какое время затратил катер на путь от А до В и на путь от В до А. Время движения из А в В выражается дробью [[Image:14-06-9.jpg|Дробь]]. Подставив вместо х число 4, получим [[Image:14-06-19.jpg|320px|Задание]], т. е. <br> |
| | + | |
| | + | [[Image:14-06-19.jpg|320px|Задание]]<br><br>Время движения катера из В в А выражается дробью [[Image:14-06-10.jpg|Дробь]]<br>Подставив вместо х число 4, получим [[Image:14-06-20.jpg]], т.е. 5 ч. <br>О т в е т: 3 ч 20 мин; 5 ч. <br> |
| | + | |
| | + | Разумеется, не следует считать, что мы с вами можем решать задачи только на равномерное движение, как в примерах 1 и 2. <br> |
| | + | |
| | + | С помощью рациональных уравнений моделируются самые разные ситуации и общая схема решения таких задач по сути дела одна и та же. В этом мы сейчас и убедимся. <br> |
| | + | |
| | + | '''Пример 3.''' Периметр прямоугольного '''[[Задачі до теми Лічба в межах 20. Розв’язування задач на віднімання. Розпізнавання трикутників|треугольника]]''' равен 48 см, один его катет на 4 см больше другого. Чему равны стороны этого треугольника? <br> |
| | + | |
| | + | Решение. <br> |
| | + | |
| | + | <br><u>'''Первый этап.'''</u> Составление математической модели. <br> |
| | + | |
| | + | Пусть х см — меньший катет треугольника, тогда больший катет равен (х + 4) см. Так как периметр треугольника равен 48 см, то гипотенуза равна 48 - х - (х + 4), т. е. (44 - 2х) см. <br> |
| | + | |
| | + | [[Image:14-06-21.jpg|240px|Задание]]<br> |
| | + | |
| | + | На рис. 99 представлена геометрическая модель задачи: прямоугольный треугольник с обозначенными длинами сторон. Применив к этому треугольнику теорему Пифагора, получим х<sup>2</sup> + (х + 4)<sup>2</sup> = (44 - 2х)<sup>2</sup>. Математическая модель задачи составлена. <br> |
| | + | |
| | + | <u>'''Второй этап.'''</u> Работа с составленной моделью. <br> |
| | + | |
| | + | Последовательно находим: <br> |
| | + | |
| | + | [[Image:14-06-22.jpg|480px|Уравнение]]<br><br><u>'''Третий этап.'''</u>Ответ на вопрос задачи. <br> |
| | + | |
| | + | Спрашивается, чему равны стороны треугольника? Меньший катет мы обозначили буквой х. Для х существуют две возможности: либо х = 80 см, либо х = 12 см. Первое значение нас не устраивает. Почему? Дело в том, что одна сторона треугольника не может быть больше его периметра, а по условию периметр треугольника равен 48 см. Остается одна возможность: х = 12 см. Тогда второй катет, который на 4 см больше, равен 16 см, а гипотенуза равна |
| | + | |
| | + | 48 - 12 - 16 = 20 см. <br> |
| | + | |
| | + | Ответ: 12 см, 16 см, 20 см. <br> |
| | + | |
| | + | '''''Замечание.''''' Математическую модель только что решенной задачи можно было составить и по-другому. Пусть, как и раньше, х см — меньший катет, (x + 4) см — больший катет треугольника. Гипотенузу выразим по '''[[Теорема Вієта і теорема, обернена до неї|теореме]]''' Пифагора: |
| | + | |
| | + | [[Image:14-06-23.jpg|120px|Формула]]см. <br> |
| | + | |
| | + | Так как, по условию, периметр треугольника (т. е. сумма трех его сторон) равен 48 см, то получаем уравнение |
| | + | |
| | + | [[Image:14-06-24.jpg|320px|Уравнение]]. <br>В этом уравнении переменная содержится под знаком квадратного корня, такие уравнения называют иррациональными. Но как их решать, мы с вами пока не обсуждали. Это уравнение нам пока не по силам, вернемся к нему позднее, в § 25. |
| | + | |
| | + | '''Пример 4.''' Для вывоза со склада 80 т груза автокомбинату было заказано некоторое количество машин одинаковой грузоподъемности. Руководство комбината решило, что на каждую машину можно грузить на 1 т груза больше, чем планировали на складе, и прислало на 4 машины меньше, чем было заказано. Весь груз в итоге был вывезен. Сколько машин было заказано и сколько прислал автокомбинат? <br> |
| | + | |
| | + | Решение. <br> |
| | + | |
| | + | <br><u>'''Первый этап.'''</u> Составление математической модели. <br>Обозначим через х число машин, заказанных автокомбинату. |
| | + | |
| | + | Тогда: (х - 4) — число машин, которое прислал комбинат на самом деле; <br>[[Image:14-06-25.jpg]] т — количество груза, которое предполагалось грузить на каждую машину; <br>[[Image:14-06-26.jpg|дробь]] т — количество груза, которое помещали на каждую машину в действительности. |
| | + | |
| | + | По условию, на каждую машину поместили на 1 т груза больше, чем намечалось, т. е. величина, выражаемая дробью больше, чем намечалось, [[Image:14-06-26.jpg|дробь]], больше величины, выражаемой дробью , [[Image:14-06-25.jpg]], на 1. Таким образом, мы приходим к уравнению |
| | + | |
| | + | [[Image:14-06-27.jpg|120px|Уравнение]]<br><br>Математическая модель задачи составлена. |
| | + | |
| | + | <br> |
| | + | |
| | + | <u>'''Второй этап.'''</u> Работа с составленной моделью. <br> |
| | + | |
| | + | Последовательно имеем |
| | + | |
| | + | [[Image:14-06-28.jpg|240px|Уравнение]]<br><br>Приравняем нулю числитель полученной алгебраической дроби: - х<sup>2</sup> + 4х + 320 = 0. <br> |
| | + | |
| | + | Далее последовательно находим: х<sup>2</sup> - 4х - 320 = 0; |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:14-06-29.jpg|320px|Уравнение]]<br><br>Оба найденные значения удовлетворяют условию [[Image:14-06-30.jpg|Задание]], значит они — '''[[Степени и корни. Степенные функции. Основные результаты|корни]]''' уравнения, составленного на первом этапе. <br> |
| | + | |
| | + | <br><u>'''Третий этап.'''</u> Ответ на вопрос задачи. <br> |
| | + | |
| | + | Мы обозначили через х число машин, заказанных складом у автокомбината. Отрицательным это число быть не может, поэтому из двух корней уравнения выбираем только один: x = 20. <br> |
| | + | |
| | + | Таким образом, заказывали 20 машин, а прислано было на 4 машины меньше, т. е. 16 машин. <br> |
| | + | |
| | + | О т в е т: 20 машин, 16 машин. |
| | + | |
| | + | '''Пример 5'''. В райцентре два кинотеатра — «Факел» и «Слава», первый — на 400, а второй — на 600 мест. В зрительном зале кинотеатра «Слава» на 4 ряда больше, чем в зрительном зале кинотеатра «Факел», и, кроме того, в каждом ряду на 5 мест больше, чем в кинотеатре «Факел». Сколько рядов в зрительном зале кинотеатра «Факел», если известно, что в каждом ряду кинотеатра «Слава» более 25 мест? <br> |
| | + | |
| | + | Решение. <br> |
| | + | |
| | + | <br><u>'''Первый этап'''</u>. Составление математической модели. <br> |
| | | | |
| - | [[Image:14-06-15.jpg]]<br><br>Выполним дальнейшие преобразования: <br> | + | Пусть х — число рядов в кинотеатре «Факел». Тогда х + 4 — число рядов в кинотеатре «Слава»; 400 д <br>[[Image:14-06-33.jpg|число]] число мест в каждом ряду кинотеатра «Факел»; <br>[[Image:14-06-34.jpg|число]] число мест в каждом ряду кинотеатра «Слава». <br>По условию, в каждом ряду кинотеатра «Слава» на 5 мест больше, чем в каждом ряду кинотеатра «Факел». Следовательно, |
| | | | |
| - | [[Image:14-06-16.jpg]]<br>[[Image:14-06-17.jpg]]<br> Из уравнения 5х<sup>2</sup> - 80 = 0 находим х<sup>2</sup> = 16, х<sub>1,2</sub> = ± 4. <br>Оба эти значения удовлетворяют условию [[Image:14-06-18.jpg]], значит, они являются корнями составленного рационального уравнения. <br><u>'''Третий этап.'''</u> Ответ на вопрос задачи. <br><u>Во-первых</u>, за х мы приняли скорость течения реки, а отрицательным числом скорость выражаться не может. Значит, из двух значений 4 и - 4 выбираем первое и отбрасываем второе. <br> | + | [[Image:14-06-35.jpg|120px|Решение]]<br><br>Математическая модель составлена. Это — рациональное уравнение. |
| | | | |
| - | <u>Во-вторых</u>, нас не спрашивают, чему равна скорость течения реки, а спрашивают, какое время затратил катер на путь от А до В и на путь от В до А. Время движения из А в В выражается дробью [[Image:14-06-9.jpg]]. Подставив вместо х число 4, получим [[Image:14-06-19.jpg]], т. е. <br> | + | <u>'''Второй этап.'''</u> Работа с составленной '''[[Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций |моделью]]'''. |
| | | | |
| - | [[Image:14-06-19.jpg]]<br><br>Время движения катера из В в А выражается дробью [[Image:14-06-10.jpg]]<br>Подставив вместо х число 4, получим [[Image:14-06-20.jpg]], т.е. 5 ч. <br>О т в е т: 3 ч 20 мин; 5 ч. <br>
| + | Решив составленное рациональное уравнение (выкладки мы не приводим, поскольку аналогичное уравнение было только что решено в предыдущем примере), получим х<sub>1</sub> = 20, х<sub>2</sub>= 16. |
| | | | |
| - | Разумеется, не следует считать, что мы с вами можем решать задачи только на равномерное движение, как в примерах 1 и 2. <br>С помощью рациональных уравнений моделируются самые разные ситуации и общая схема решения таких задач по сути дела одна и та же. В этом мы сейчас и убедимся. <br>
| + | <u>'''Третий этап.'''</u> Ответ на вопрос задачи. |
| | | | |
| - | '''Пример 3.''' Периметр прямоугольного треугольника равен 48 см, один его катет на 4 см больше другого. Чему равны стороны этого треугольника? <br>Решение. <br><u>'''Первый этап.'''</u> Составление математической модели. <br>Пусть х см — меньший катет треугольника, тогда больший катет равен (х + 4) см. Так как периметр треугольника равен 48 см, то гипотенуза равна 48 - х - (х + 4), т. е. (44 - 2х) см. <br>
| + | За х мы приняли число рядов в кинотеатре «Факел». В соответствии с полученными решениями мы должны проанализировать две возможности: либо в кинотеатре «Факел» 20 рядов и, значит, 20 мест в каждом ряду (поскольку в кинотеатре «Факел» всего 400 мест в зрительном зале), либо в этом кинотеатре 16 рядов по 25 мест в каждом ряду. Если выбрать первую возможность, то в кинотеатре «Слава» будет 24 ряда (согласно условию, в кинотеатре «Слава» на 4 ряда больше) по 25 мест в каждом ряду (согласно условию, в каждом ряду кинотеатра «Слава» на 5 мест больше, чем в кинотеатре «Факел»). Это нас не устраивает, так как по условию в каждом ряду кинотеатра «Слава» более 25 мест. Рассмотрим вторую возможность: в кинотеатре «Факел» 16 рядов по 25 мест в каждом. Тогда в кинотеатре «Слава» будет 20 рядов по 30 мест в каждом. Это нас устраивает. |
| | | | |
| - | [[Image:14-06-21.jpg]]<br>
| + | Итак, из двух указанных возможностей выбираем вторую, а это означает, что в кинотеатре «Факел» 16 рядов. |
| | | | |
| - | На рис. 99 представлена геометрическая модель задачи: прямоугольный треугольник с обозначенными длинами сторон. Применив к этому треу- <br>гольнику теорему Пифагора, получим х<sup>2</sup> + (х + 4)<sup>2</sup> = (44 - 2х)<sup>2</sup>. Математическая модель задачи составлена. <br>
| + | Ответ: 16 рядов. |
| | | | |
| - | <u>'''Второй этап.'''</u> Работа с составленной моделью. <br>Последовательно находим: <br>
| + | '''Пример 6. '''Задумано двузначное число. Известно, что: |
| | | | |
| - | [[Image:14-06-22.jpg]]<br><br><u>'''Третий этап.'''</u>Ответ на вопрос задачи. <br>Спрашивается, чему равны стороны треугольника? Меньший катет мы обозначили буквой х. Для х существуют две возможности: либо х = 80 см, либо х = 12 см. Первое значение нас не устраивает. Почему? Дело в том, что одна сторона треугольника не может быть больше его периметра, а по условию периметр треугольника равен 48 см. Остается одна возможность: х = 12 см. Тогда второй катет, который на 4 см больше, равен 16 см, а гипотенуза равна
| + | 1) сумма квадратов цифр задуманного числа равна 58; <br>2) если цифры задуманного числа поменять местами, то получится '''[[Загадка до уроку на тему «Читання, запис та порівняння чисел. Одноцифрові та двоцифрові числа. Число попереднє та наступне до даного»|двузначное число]]''', которое больше задуманного на 36. |
| | | | |
| - | 48 - 12 - 16 = 20 см. <br>Ответ: 12 см, 16 см, 20 см. <br>'''''Замечание.''''' Математическую модель только что решенной задачи можно было составить и по-другому. Пусть, как и раньше, х см — меньший катет, <br>(x + 4) см — больший катет треугольника. Гипотенузу выразим по теореме Пифагора:
| + | Какое число задумано? |
| | | | |
| - | [[Image:14-06-23.jpg]]см. <br>Так как, по условию, периметр треугольника (т. е. сумма трех его сторон) равен 48 см, то получаем уравнение
| + | Решение. |
| | | | |
| - | [[Image:14-06-24.jpg]]. <br>В этом уравнении переменная содержится под знаком квадратного корня, такие уравнения называют иррациональными. Но как их решать, мы с вами пока не обсуждали. Это уравнение нам пока не по силам, вернемся к нему позднее, в § 25.
| + | <u>'''Первый этап.'''</u> Составление математической модели. |
| | | | |
| - | '''Пример 4.''' Для вывоза со склада 80 т груза автокомбинату было заказано некоторое количество машин одинаковой грузоподъемности. Руководство комбината решило, что на каждую машину можно грузить на 1 т груза больше, чем планировали на складе, и прислало на 4 машины меньше, чем было заказано. Весь груз в итоге был вывезен. Сколько машин было заказано и сколько прислал автокомбинат? <br>Решение. <br><u>'''Первый этап.'''</u> Составление математической модели. <br>Обозначим через х число машин, заказанных автокомбинату.
| + | Для перевода ситуации с обыденного языка на математический придется ввести не одну, а две переменные: х — цифра десятков, у — цифра единиц задуманного числа. Само задуманное число имеет вид 10x + у. Если же цифры поменять местами, то получится число 10y + х. |
| | | | |
| - | Тогда: (х - 4) — число машин, которое прислал комбинат на самом деле; <br>[[Image:14-06-25.jpg]] т — количество груза, которое предполагалось грузить на каждую машину; <br>[[Image:14-06-26.jpg]] т — количество груза, которое помещали на каждую машину в действительности.
| + | Согласно первому условию, сумма квадратов цифр задуманного числа равна 58; это значит, что х<sup>2</sup> + у<sup>2</sup> = 58. <br>Далее, согласно второму условию, если '''[[Ілюстрації: Лічба предметів. Порівняння предметів за величиною. Підготовчі вправи до написання цифр.|цифры]]''' задуманного числа поменять местами, то получится число (оно, как мы отметили выше, имеет вид 10y + x), которое больше задуманного (т. е. числа 10x + у) на 36. Это значит, что <br>10(y + х) - (10x + у) = 36, откуда после упрощений получим у - х = 4. <br>Таким образом, математическая модель задачи представляет собой систему уравнений: |
| | | | |
| - | По условию, на каждую машину поместили на 1 т груза больше, чем намечалось, т. е. величина, выражаемая дробью больше, чем намечалось, [[Image:14-06-26.jpg]], больше величины, выражаемой дробью , [[Image:14-06-25.jpg]], на 1. Таким образом, мы приходим к уравнению
| + | [[Image:14-06-36.jpg|120px|Уравнение]]<br><br><u>'''Второй этап.'''</u> Работа с составленной моделью. |
| | | | |
| - | [[Image:14-06-27.jpg]]<br><br>Математическая модель задачи составлена.
| + | Вообще говоря, такие системы уравнений мы с вами пока не решали. Более того, изучение систем уравнений — тема 9-го класса. Так что же нам делать: отложить эту задачу до следующего года или, опережая события, попытаться ее решить уже сейчас, тем более что некоторое знакомство с системами уравнений у нас состоялось в курсе алгебры 7-го класса? Не будем откладывать. Воспользуемся методом подстановки: выразим у через х из второго уравнения и подставим полученное выражение вместо у в первое уравнение. |
| | | | |
| - | <u>'''Второй этап.'''</u> Работа с составленной моделью. <br>Последовательно имеем
| + | 1) Из второго уравнения системы выразим у: у = х + 4. |
| | | | |
| - | [[Image:14-06-28.jpg]]<br><br>Приравняем нулю числитель полученной алгебраической <br>дроби: <br>- х<sup>2</sup> + 4х + 320 = 0. <br>Далее последовательно находим: <br>х<sup>2</sup> - 4х - 320 = 0;
| + | 2) Подставим полученное выражение вместо у в первое уравнение системы: |
| | | | |
| - | [[Image:14-06-29.jpg]]<br><br>Оба найденные значения удовлетворяют условию [[Image:14-06-30.jpg]], значит они — корни уравнения, составленного на первом этапе. <br><u>'''Третий этап.'''</u> Ответ на вопрос задачи. <br>Мы обозначили через х число машин, заказанных складом у автокомбината. Отрицательным это число быть не может, поэтому из двух корней уравнения выбираем только один: x = 20. <br>Таким образом, заказывали 20 машин, а прислано было на 4 машины меньше, т. е. 16 машин. <br>О т в е т: 20 машин, 16 машин.
| + | х<sup>2</sup> + (х + 4)<sup>2</sup> = 58. |
| | | | |
| - | '''Пример 5'''. В райцентре два кинотеатра — «Факел» и «Слава», первый — на 400, а второй — на 600 мест. В зрительном зале кинотеатра «Слава» на 4 ряда больше, чем в зрительном зале кинотеатра «Факел», и, кроме того, в каждом ряду на 5 мест больше, чем в кинотеатре «Факел». Сколько рядов в зрительном <br>зале кинотеатра «Факел», если известно, что в каждом ряду кинотеатра «Слава» более 25 мест? <br>Решение. <br><u>'''Первый этап'''</u>. Составление математической модели. <br>Пусть х — число рядов в кинотеатре «Факел». Тогда х + 4 — число рядов в кинотеатре «Слава»; <br>400 д <br>[[Image:14-06-33.jpg]] число мест в каждом ряду кинотеатра «Факел»; <br>[[Image:14-06-34.jpg]] число мест в каждом ряду кинотеатра «Слава». <br>По условию, в каждом ряду кинотеатра «Слава» на 5 мест больше, чем в каждом ряду кинотеатра «Факел». Следовательно,
| + | 3) Решим полученное уравнение: |
| | | | |
| - | [[Image:14-06-35.jpg]]<br><br>Математическая модель составлена. Это — рациональное уравнение.
| + | х<sup>2</sup> + (х<sup>2</sup> + 8х + 16) = 58; <br>2х<sup>2</sup> + 8х + 16 - 58 = 0; <br>2х<sup>2</sup> + 8х - 42 = 0; <br>x<sup>2</sup> + 4x - 21 = 0; <br>х<sub>1</sub> = 3, х<sub>2</sub> = — 7. |
| | | | |
| - | <u>'''Второй этап.'''</u> Работа с составленной моделью. <br>Решив составленное рациональное уравнение (выкладки мы не приводим, поскольку аналогичное уравнение было только что решено в предыдущем примере), получим х<sub>1</sub> = 20, х<sub>2</sub>= 16.
| + | 4) Подставим поочередно каждое из найденных значений х в '''[[Конспект уроку на тему «Формула коренів квадратного рівняння»|формулу]]''' у = х + 4. Если х = 3, то у = 3 + 4 = 7; если х = - 7, то y = -7 + 4 = -3. |
| | | | |
| - | <u>'''Третий этап.'''</u> Ответ на вопрос задачи. <br>За х мы приняли число рядов в кинотеатре «Факел». В соответствии с полученными решениями мы должны проанализировать две возможности: либо в кинотеатре «Факел» 20 рядов и, значит, 20 мест в каждом ряду (поскольку в кинотеатре «Факел» всего 400 мест в зрительном зале), либо в этом кинотеатре 16 рядов по 25 мест в каждом ряду. Если выбрать первую возможность, то в кинотеатре «Слава» будет 24 ряда (согласно условию, в кинотеатре «Слава» на 4 ряда больше) по 25 мест в каждом ряду (согласно условию, в каждом ряду кинотеатра «Слава» на 5 мест больше, чем в кинотеатре «Факел»). Это нас <br>не устраивает, так как по условию в каждом ряду кинотеатра «Слава» более 25 мест. Рассмотрим вторую возможность: в кинотеатре «Факел» 16 рядов по 25 мест в каждом. Тогда в кинотеатре «Слава» будет 20 рядов по 30 мест в каждом. Это нас устраивает. <br>Итак, из двух указанных возможностей выбираем вторую, а это означает, что в кинотеатре «Факел» 16 рядов. <br>Ответ: 16 рядов.
| + | 5) Пары (3; 7) и (- 7; - 3) — решения заданной системы уравнений. |
| | | | |
| - | '''Пример 6. '''Задумано двузначное число. Известно, что: <br>1) сумма квадратов цифр задуманного числа равна 58; <br>2) если цифры задуманного числа поменять местами, то получится двузначное число, которое больше задуманного на 36. <br>Какое число задумано? <br>Решение. <br><u>'''Первый этап.'''</u> Составление математической модели. <br>Для перевода ситуации с обыденного языка на математический придется ввести не одну, а две переменные: х — цифра десятков, у — цифра единиц задуманного числа. Само задуманное число имеет вид 10x + у. Если же цифры поменять местами, то получится число 10y + х. <br>Согласно первому условию, сумма квадратов цифр задуманного числа равна 58; это значит, что х<sup>2</sup> + у<sup>2</sup> = 58. <br>Далее, согласно второму условию, если цифры задуманного числа поменять местами, то получится число (оно, как мы отметили выше, имеет вид 10y + x), которое больше задуманного (т. е. числа 10x + у) на 36. Это значит, что <br>10(y + х) - (10x + у) = 36, откуда после упрощений получим у - х = 4. <br>Таким образом, математическая модель задачи представляет собой систему уравнений: [[Image:14-06-36.jpg]]<br><br><u>'''Второй этап.'''</u> Работа с составленной моделью. <br>Вообще говоря, такие системы уравнений мы с вами пока не решали. Более того, изучение систем уравнений — тема 9-го класса. Так что же нам делать: отложить эту задачу до следующего года или, опережая события, попытаться ее решить уже сейчас, тем более что некоторое знакомство с системами <br>уравнений у нас состоялось в курсе алгебры 7-го класса? Не будем откладывать. Воспользуемся методом подстановки: выразим у через х из второго уравнения и подставим полученное выражение вместо у в первое уравнение.
| + | <u>'''Третий этап.'''</u> Ответ на вопрос задачи. |
| | | | |
| - | 1) Из второго уравнения системы выразим у: у = х + 4. <br>2) Подставим полученное выражение вместо у в первое уравнение системы: <br>х<sup>2</sup> + (х + 4)<sup>2</sup> = 58. <br>3) Решим полученное уравнение: <br>х<sup>2</sup> + (х<sup>2</sup> + 8х + 16) = 58; <br>2х<sup>2</sup> + 8х + 16 - 58 = 0; <br>2х<sup>2</sup> + 8х - 42 = 0; <br>x<sup>2</sup> + 4x - 21 = 0; <br>х<sub>1</sub> = 3, х<sub>2</sub> = — 7. <br>4) Подставим поочередно каждое из найденных значений х в формулу у = х + 4. Если х = 3, то у = 3 + 4 = 7; если х = - 7, то y = -7 + 4 = -3. <br>5) Пары (3; 7) и (- 7; - 3) — решения заданной системы уравнений.
| + | По условию, х и у — цифры двузначного числа. Отрицательными цифры быть не могут, значит, пара (- 7; - 3) не подходит как не соответствующая условию задачи. Остается пара (3; 7), т. е. х = 3, у = 7. Здесь переменные х и у имеют следующий смысл: х — цифра десятков, а у — цифра единиц задуманного двузначного числа. Значит, было задумано число 37. |
| | | | |
| - | <u>'''Третий этап.'''</u> Ответ на вопрос задачи. <br>По условию, х и у — цифры двузначного числа. Отрицательными цифры быть не могут, значит, пара (- 7; - 3) не подходит как не соответствующая условию задачи. Остается пара (3; 7), т. е. х = 3, у = 7. Здесь переменные х и у имеют следующий смысл: х — цифра десятков, а у — цифра единиц задуманного <br>двузначного числа. Значит, было задумано число 37. <br>Ответ: 37. <br>
| + | Ответ: 37. <br> |
| | | | |
| | <br> ''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. '' | | <br> ''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. '' |
Текущая версия на 12:41, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Рациональные уравнения как математические модели реальных ситуаций
Рациональные уравнения как математические модели реальных ситуаций
То, что рациональные уравнения могут служить математическими моделями реальных ситуаций, вам известно, целый ряд соответствующих примеров мы рассмотрели выше в § 7 и ранее, в учебнике «Алгебра-7». Сейчас поговорим об этом более подробно.
Пример 1. Перегон в 60 км поезд должен был проехать с постоянной скоростью за определенное расписанием время. Простояв у семафора перед перегоном 5 мин, машинист вынужден был увеличить скорость прохождения перегона на 10 км/ч, чтобы наверстать к окончанию прохождения перегона потерянные 5 мин. С какой скоростью поезд должен был пройти перегон по расписанию?
Решение.
Первый этап. Составление математической модели. Пусть х км/ч — скорость поезда по расписанию. Так как протяженность перегона равна 60 км, то время, отведенное расписанием на прохождение перегона, составляет 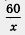 ч. ч.
Фактически поезд прошел перегон в 60 км со скоростью (х + 10) км/ч, значит, время, затраченное на прохождение перегона, равно 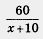 ч. ч.
Из двух величин — 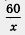 ч и ч и 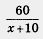 ч первая больше второй на 5 мин, т. е. на ч первая больше второй на 5 мин, т. е. на 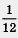 ч. Значит, мы приходим к уравнению ч. Значит, мы приходим к уравнению
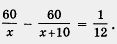
Математическая модель задачи составлена. Это — рациональное уравнение.
Второй этап. Работа с составленной моделью.
Имеем
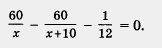
Преобразуем левую часть уравнения
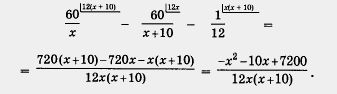
Приравняв числитель этой дроби нулю, получим квадратное уравнение - х2 - 10х + 7200 = 0 или, переходя к более удобной записи, х2 + 10х - 7200 = 0.
Применяя известную формулу, находим
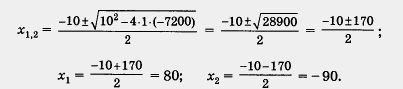
Оба значения удовлетворяют условию 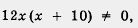 , следовательно, эти значения — корни составленного рационального уравнения. <u</u> , следовательно, эти значения — корни составленного рационального уравнения. <u</u>
Третий этап. Ответ на вопрос задачи.
Спрашивается, с какой скоростью поезд должен был пройти перегон по расписанию? Именно эту величину мы обозначили значение нас явно не устраивает, поскольку скорость движения поезда не может выражаться отрицательным числом. Значит, выбираем значение х = 80, это и есть ответ на вопрос задачи.
О т в е т: 80 км/ч.
Сделаем некоторые комментарии к выполненному решению.
1. Конечно, рассмотренная ситуация несколько идеализирована: вряд ли в реальной жизни поезд пройдет весь перегон с постоянной скоростью, ведь всегда есть и ускорения, и замедления. Но на такую идеализацию математикам приходится идти сознательно.
2. В очередной раз обращаем ваше внимание на то, что мы воспользовались привычной схемой рассуждений: составление математической модели, работа с составленной моделью, ответ на вопрос задачи.
3. Подчеркнем, что первый этап, т. е. составление математической модели, — ключевой в решении задачи. На этом этапе осуществляется перевод условия задачи с обыденного языка на математический язык, т. е. выполняется серьезная творческая работа. Серьезная работа проводится и на втором этапе, но эта работа не творческая, а чисто техническая, поскольку, действуя по алгоритму, особенно думать не приходится.
Вернемся к рассмотренной задаче и проанализируем, как осуществляется перевод с обыденного языка на математический.
Искомую величину мы обозначили буквой х. Это дало нам возможность оперировать с искомой скоростью, ведь с точки зрения алгебры не важно, имеем ли мы дело с числами или с буквами.
Зная путь 60 км) и скорость (х км/ч) и использовав физический закон равномерного движения s = vt (s — путь, v — скорость, t — время), мы нашли время, предусмотренное расписанием, — оно выражается дробью 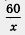 ч. ч.
По условию, перегон был пройден со скоростью, на 10 км/ч большей, чем предполагалось расписанием. Перевод этого условия на математический язык дал следующее: (х + 10) км/ч — фактическая скорость прохождения перегона, а 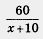 ч — фактическое время движения поезда по перегону в 60 км. ч — фактическое время движения поезда по перегону в 60 км.
Далее, согласно условию, на рассматриваемом перегоне поезд выиграл, по сравнению с расписанием, 5 мин, т. е. 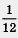 ч. ч.
Иными словами, время, предусмотренное расписанием (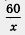 ч ), больше фактического времени ч ), больше фактического времени 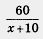 ч ) на ч ) на 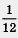 ч. ч.
На математическом языке это означает, что 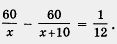 (из большей величины вычли меньшую и получили указанную в условии разность). (из большей величины вычли меньшую и получили указанную в условии разность).
Обратите внимание на то, что сравнивать надо величины одного и того же наименования (в данном уравнении это — часы).
Пример 2. Пристани А и В расположены на реке, причем В — на 80 км ниже по течению, чем А. Катер прошел путь из А в В и обратно за 8 ч 20 мин. За какое время катер прошел расстояние от А до В и расстояние от В до А, если известно, что его собственная скорость (скорость в стоячей воде) равна 20 км/ч?
Решение.
Первый этап. Составление математической модели.
Пусть х км/ч — скорость течения реки. Тогда: (20 + х) км/ч — скорость движения катера по течению;
(20 - х) км/ч — скорость движения катера против течения; 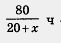 — время движения катера по течению; — время движения катера по течению;
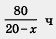 время движения катера против течения. время движения катера против течения.
По условию, на путь туда и обратно катер затратил 8 ч 20 мин, т. е. 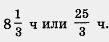 Но время, затраченное катером на путь из А в В и обратно, выражается суммой дробей Но время, затраченное катером на путь из А в В и обратно, выражается суммой дробей 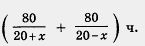
Значит, мы приходим к уравнению
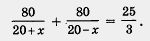
Перевод условий задачи с обыденного языка на математический состоялся, математическая модель составлена. Это — рациональное уравнение.
Второй этап. Работа с составленной моделью.
Имеем
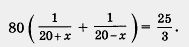
Есть смысл разделить обе части уравнения на 5, хотя бы для того, чтобы облегчить последующие вычисления:
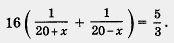
Выполним дальнейшие преобразования:
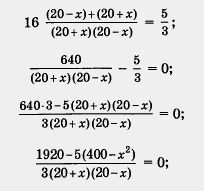
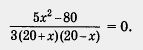
Из уравнения 5х2 - 80 = 0 находим х2 = 16, х1,2 = ± 4.
Оба эти значения удовлетворяют условию 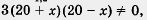 , значит, они являются корнями составленного рационального уравнения. , значит, они являются корнями составленного рационального уравнения.
Третий этап. Ответ на вопрос задачи.
Во-первых, за х мы приняли скорость течения реки, а отрицательным числом скорость выражаться не может. Значит, из двух значений 4 и - 4 выбираем первое и отбрасываем второе.
Во-вторых, нас не спрашивают, чему равна скорость течения реки, а спрашивают, какое время затратил катер на путь от А до В и на путь от В до А. Время движения из А в В выражается дробью 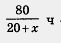 . Подставив вместо х число 4, получим . Подставив вместо х число 4, получим  , т. е. , т. е.

Время движения катера из В в А выражается дробью 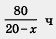
Подставив вместо х число 4, получим 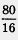 , т.е. 5 ч. , т.е. 5 ч.
О т в е т: 3 ч 20 мин; 5 ч.
Разумеется, не следует считать, что мы с вами можем решать задачи только на равномерное движение, как в примерах 1 и 2.
С помощью рациональных уравнений моделируются самые разные ситуации и общая схема решения таких задач по сути дела одна и та же. В этом мы сейчас и убедимся.
Пример 3. Периметр прямоугольного треугольника равен 48 см, один его катет на 4 см больше другого. Чему равны стороны этого треугольника?
Решение.
Первый этап. Составление математической модели.
Пусть х см — меньший катет треугольника, тогда больший катет равен (х + 4) см. Так как периметр треугольника равен 48 см, то гипотенуза равна 48 - х - (х + 4), т. е. (44 - 2х) см.
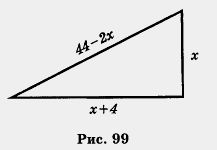
На рис. 99 представлена геометрическая модель задачи: прямоугольный треугольник с обозначенными длинами сторон. Применив к этому треугольнику теорему Пифагора, получим х2 + (х + 4)2 = (44 - 2х)2. Математическая модель задачи составлена.
Второй этап. Работа с составленной моделью.
Последовательно находим:

Третий этап.Ответ на вопрос задачи.
Спрашивается, чему равны стороны треугольника? Меньший катет мы обозначили буквой х. Для х существуют две возможности: либо х = 80 см, либо х = 12 см. Первое значение нас не устраивает. Почему? Дело в том, что одна сторона треугольника не может быть больше его периметра, а по условию периметр треугольника равен 48 см. Остается одна возможность: х = 12 см. Тогда второй катет, который на 4 см больше, равен 16 см, а гипотенуза равна
48 - 12 - 16 = 20 см.
Ответ: 12 см, 16 см, 20 см.
Замечание. Математическую модель только что решенной задачи можно было составить и по-другому. Пусть, как и раньше, х см — меньший катет, (x + 4) см — больший катет треугольника. Гипотенузу выразим по теореме Пифагора:
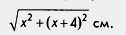 см. см.
Так как, по условию, периметр треугольника (т. е. сумма трех его сторон) равен 48 см, то получаем уравнение
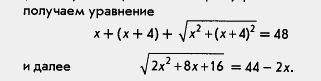 . .
В этом уравнении переменная содержится под знаком квадратного корня, такие уравнения называют иррациональными. Но как их решать, мы с вами пока не обсуждали. Это уравнение нам пока не по силам, вернемся к нему позднее, в § 25.
Пример 4. Для вывоза со склада 80 т груза автокомбинату было заказано некоторое количество машин одинаковой грузоподъемности. Руководство комбината решило, что на каждую машину можно грузить на 1 т груза больше, чем планировали на складе, и прислало на 4 машины меньше, чем было заказано. Весь груз в итоге был вывезен. Сколько машин было заказано и сколько прислал автокомбинат?
Решение.
Первый этап. Составление математической модели.
Обозначим через х число машин, заказанных автокомбинату.
Тогда: (х - 4) — число машин, которое прислал комбинат на самом деле;
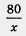 т — количество груза, которое предполагалось грузить на каждую машину; т — количество груза, которое предполагалось грузить на каждую машину;
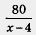 т — количество груза, которое помещали на каждую машину в действительности. т — количество груза, которое помещали на каждую машину в действительности.
По условию, на каждую машину поместили на 1 т груза больше, чем намечалось, т. е. величина, выражаемая дробью больше, чем намечалось, 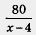 , больше величины, выражаемой дробью , , больше величины, выражаемой дробью , 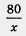 , на 1. Таким образом, мы приходим к уравнению , на 1. Таким образом, мы приходим к уравнению
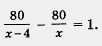
Математическая модель задачи составлена.
Второй этап. Работа с составленной моделью.
Последовательно имеем
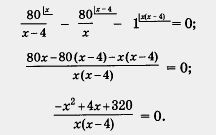
Приравняем нулю числитель полученной алгебраической дроби: - х2 + 4х + 320 = 0.
Далее последовательно находим: х2 - 4х - 320 = 0;
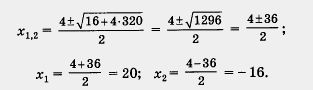
Оба найденные значения удовлетворяют условию 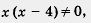 , значит они — корни уравнения, составленного на первом этапе. , значит они — корни уравнения, составленного на первом этапе.
Третий этап. Ответ на вопрос задачи.
Мы обозначили через х число машин, заказанных складом у автокомбината. Отрицательным это число быть не может, поэтому из двух корней уравнения выбираем только один: x = 20.
Таким образом, заказывали 20 машин, а прислано было на 4 машины меньше, т. е. 16 машин.
О т в е т: 20 машин, 16 машин.
Пример 5. В райцентре два кинотеатра — «Факел» и «Слава», первый — на 400, а второй — на 600 мест. В зрительном зале кинотеатра «Слава» на 4 ряда больше, чем в зрительном зале кинотеатра «Факел», и, кроме того, в каждом ряду на 5 мест больше, чем в кинотеатре «Факел». Сколько рядов в зрительном зале кинотеатра «Факел», если известно, что в каждом ряду кинотеатра «Слава» более 25 мест?
Решение.
Первый этап. Составление математической модели.
Пусть х — число рядов в кинотеатре «Факел». Тогда х + 4 — число рядов в кинотеатре «Слава»; 400 д
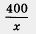 число мест в каждом ряду кинотеатра «Факел»; число мест в каждом ряду кинотеатра «Факел»;
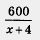 число мест в каждом ряду кинотеатра «Слава». число мест в каждом ряду кинотеатра «Слава».
По условию, в каждом ряду кинотеатра «Слава» на 5 мест больше, чем в каждом ряду кинотеатра «Факел». Следовательно,
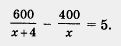
Математическая модель составлена. Это — рациональное уравнение.
Второй этап. Работа с составленной моделью.
Решив составленное рациональное уравнение (выкладки мы не приводим, поскольку аналогичное уравнение было только что решено в предыдущем примере), получим х1 = 20, х2= 16.
Третий этап. Ответ на вопрос задачи.
За х мы приняли число рядов в кинотеатре «Факел». В соответствии с полученными решениями мы должны проанализировать две возможности: либо в кинотеатре «Факел» 20 рядов и, значит, 20 мест в каждом ряду (поскольку в кинотеатре «Факел» всего 400 мест в зрительном зале), либо в этом кинотеатре 16 рядов по 25 мест в каждом ряду. Если выбрать первую возможность, то в кинотеатре «Слава» будет 24 ряда (согласно условию, в кинотеатре «Слава» на 4 ряда больше) по 25 мест в каждом ряду (согласно условию, в каждом ряду кинотеатра «Слава» на 5 мест больше, чем в кинотеатре «Факел»). Это нас не устраивает, так как по условию в каждом ряду кинотеатра «Слава» более 25 мест. Рассмотрим вторую возможность: в кинотеатре «Факел» 16 рядов по 25 мест в каждом. Тогда в кинотеатре «Слава» будет 20 рядов по 30 мест в каждом. Это нас устраивает.
Итак, из двух указанных возможностей выбираем вторую, а это означает, что в кинотеатре «Факел» 16 рядов.
Ответ: 16 рядов.
Пример 6. Задумано двузначное число. Известно, что:
1) сумма квадратов цифр задуманного числа равна 58;
2) если цифры задуманного числа поменять местами, то получится двузначное число, которое больше задуманного на 36.
Какое число задумано?
Решение.
Первый этап. Составление математической модели.
Для перевода ситуации с обыденного языка на математический придется ввести не одну, а две переменные: х — цифра десятков, у — цифра единиц задуманного числа. Само задуманное число имеет вид 10x + у. Если же цифры поменять местами, то получится число 10y + х.
Согласно первому условию, сумма квадратов цифр задуманного числа равна 58; это значит, что х2 + у2 = 58.
Далее, согласно второму условию, если цифры задуманного числа поменять местами, то получится число (оно, как мы отметили выше, имеет вид 10y + x), которое больше задуманного (т. е. числа 10x + у) на 36. Это значит, что
10(y + х) - (10x + у) = 36, откуда после упрощений получим у - х = 4.
Таким образом, математическая модель задачи представляет собой систему уравнений:
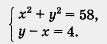
Второй этап. Работа с составленной моделью.
Вообще говоря, такие системы уравнений мы с вами пока не решали. Более того, изучение систем уравнений — тема 9-го класса. Так что же нам делать: отложить эту задачу до следующего года или, опережая события, попытаться ее решить уже сейчас, тем более что некоторое знакомство с системами уравнений у нас состоялось в курсе алгебры 7-го класса? Не будем откладывать. Воспользуемся методом подстановки: выразим у через х из второго уравнения и подставим полученное выражение вместо у в первое уравнение.
1) Из второго уравнения системы выразим у: у = х + 4.
2) Подставим полученное выражение вместо у в первое уравнение системы:
х2 + (х + 4)2 = 58.
3) Решим полученное уравнение:
х2 + (х2 + 8х + 16) = 58;
2х2 + 8х + 16 - 58 = 0;
2х2 + 8х - 42 = 0;
x2 + 4x - 21 = 0;
х1 = 3, х2 = — 7.
4) Подставим поочередно каждое из найденных значений х в формулу у = х + 4. Если х = 3, то у = 3 + 4 = 7; если х = - 7, то y = -7 + 4 = -3.
5) Пары (3; 7) и (- 7; - 3) — решения заданной системы уравнений.
Третий этап. Ответ на вопрос задачи.
По условию, х и у — цифры двузначного числа. Отрицательными цифры быть не могут, значит, пара (- 7; - 3) не подходит как не соответствующая условию задачи. Остается пара (3; 7), т. е. х = 3, у = 7. Здесь переменные х и у имеют следующий смысл: х — цифра десятков, а у — цифра единиц задуманного двузначного числа. Значит, было задумано число 37.
Ответ: 37.
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
онлайн библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|