|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Перпендикулярные прямые</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Перпендикулярные прямые, полупрямые, смежные, полуплоскость, точка пересечения</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Перпендикулярные прямые''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Перпендикулярные прямые''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ''' | + | ''' '''[[Перпендикулярные прямые. Полные уроки|'''Перпендикулярные прямые''']] |
| | | | |
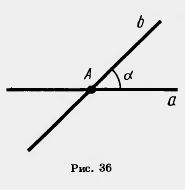
| - | <br>Пусть а и b — прямые, пересекающиеся в точке А (рис. 36). | + | <br>Пусть а и b — прямые, пересекающиеся в точке А (рис. 36). |
| | | | |
| - | [[Image:20-06-67.jpg]] | + | [[Image:20-06-67.jpg|240px|а и b — прямые, пересекающиеся в точке А]] |
| | | | |
| - | Каждая из этих прямых точкой А делится на две полупрямые. Полупрямые одной прямой образуют с полупрямыми другой прямой четыре угла. Пусть а — один из этих углов. Тогда любой из остальных трех углов будет либо смежным с углом а, либо вертикальным с углом а. Отсюда следует, что если один из углов прямой, то остальные углы тоже прямые. В этом случае мы говорим, что прямые пересекаются под прямым углом. | + | Каждая из этих прямых точкой А делится на две '''[[Полупрямая|полупрямые]]'''. Полупрямые одной прямой образуют с полупрямыми другой прямой четыре угла. Пусть а — один этих углов. Тогда любой из остальных трех углов будет либо '''[[Смежные углы. Полные уроки|смежным]]''' с углом а, либо вертикальным с углом а. Отсюда следует, что если один из углов прямой, то остальные углы тоже прямые. В этом случае мы говорим, что прямые пересекаются под прямым углом. |
| | | | |
| - | Определение. '''''Две прямые называются перпендикулярными, если они пересекаются под прямым углом''''' (рис. 37). | + | Определение. '''''Две прямые называются перпендикулярными, если они пересекаются под прямым углом''''' (рис. 37). |
| | | | |
| - | Перпендикулярность прямых обозначается знаком [[Image:20-06-68.jpg]]. Запись a[[Image:20-06-68.jpg]]b читается: "Прямая а перпендикулярна прямой b".<br>Теорема 2.3. ''Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.'' | + | Перпендикулярность прямых обозначается знаком [[Image:20-06-68.jpg|Значёк перпендикулярности прямых]]. Запись a[[Image:20-06-68.jpg|Значёк перпендикулярности прямых]]b читается: "Прямая а перпендикулярна прямой b". |
| | | | |
| - | Доказательство. Пусть а — данная прямая и А — данная точка на ней. Обозначим через Ci одну из полупрямых прямой а с начальной точкой А (рис. 38). Отложим от полупрямой Ci угол (cifei), равный 90°. Тогда прямая, содержащая луч bi, будет перпендикулярна прямой а.<br>Допустим, что существует другая прямая, тоже проходящая через точку А и перпендикулярная прямой а. Обозначим через с\ полупрямую этой прямой, лежащую в одной полуплоскости с лучом Ь|.<br>Углы (cibi) и (ciCi), равные каждый 90°, отложены в одну полуплоскость от полупрямой a<sub>1</sub>. Но от полупрямой a<sub>1</sub> в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не может быть другой прямой, проходящей через точку А и перпендикулярной прямой а. Теорема доказана.
| + | Теорема 2.3. ''Через каждую точку прямой можно провести '''[[Задачі до уроку на тему «Паралельні та перпендикулярні прямі, їх властивості. Доведення від супротивного»|перпендикулярную]]''' ей прямую, и только одну.'' |
| | | | |
| - | Определение. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.
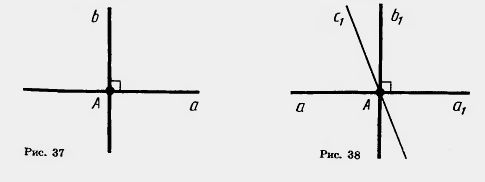
| + | Доказательство. Пусть а — данная прямая и А — данная точка на ней. Обозначим через Ci одну из полупрямых прямой а с начальной точкой А (рис. 38). Отложим от полупрямой Ci угол (cifei), равный 90°. Тогда прямая, содержащая луч bi, будет перпендикулярна прямой а. |
| | | | |
| | + | Допустим, что существует другая прямая, тоже проходящая через точку А и перпендикулярная прямой а. Обозначим через с<sub>1</sub> полупрямую этой прямой, лежащую в одной полуплоскости с лучом b<sub>1</sub>. |
| | | | |
| | + | Углы (c<sub>1</sub>b<sub>1</sub>) и (c<sub>1</sub>C<sub>1</sub>), равные каждый 90°, отложены в одну полуплоскость от полупрямой a<sub>1</sub>. Но от полупрямой a<sub>1</sub> в данную '''[[Полуплоскости|полуплоскость]]''' можно отложить только один угол, равный 90°. Поэтому не может быть другой прямой, проходящей через точку А и перпендикулярной прямой а. Теорема доказана. |
| | | | |
| - | [[Image:20-06-69.jpg]] | + | '''Определение'''. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их '''[[Точки і прямі, їх властивості. Закриті вправи|точку пересечения]]'''. Этот конец отрезка называется основанием перпендикуляра. |
| | | | |
| | + | <br> |
| | | | |
| | + | [[Image:20-06-69.jpg|550px|Перпендикулярные прямые]] |
| | | | |
| - | [[Image:20-06-70.jpg]]<br> <br>На рисунке 39 перпендикуляр АВ проведен из точки А к прямой а. Точка В — основание перпендикуляра. Для построения перпендикуляра пользуются чертежным угольником (рис. 40).
| + | <br> |
| | | | |
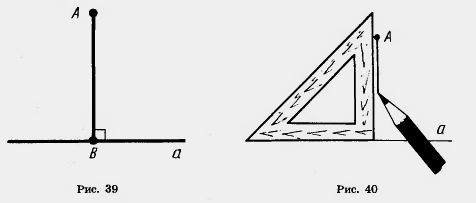
| | + | [[Image:20-06-70.jpg|550px|Перпендикулярные прямые]]<br> <br>На рисунке 39 перпендикуляр АВ проведен из точки А к прямой а. Точка В — основание перпендикуляра. Для построения перпендикуляра пользуются чертежным угольником (рис. 40). |
| | | | |
| | + | <br> |
| | | | |
| - | <br> | + | <br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | <sub>Помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], Математика для 7 класса [[Математика|скачать]], календарно-тематическое планирование</sub> | + | <br> <br> <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Определение. Две прямые называются перпендикулярными, если они пересекаются под прямым углом (рис. 37).
Доказательство. Пусть а — данная прямая и А — данная точка на ней. Обозначим через Ci одну из полупрямых прямой а с начальной точкой А (рис. 38). Отложим от полупрямой Ci угол (cifei), равный 90°. Тогда прямая, содержащая луч bi, будет перпендикулярна прямой а.
Допустим, что существует другая прямая, тоже проходящая через точку А и перпендикулярная прямой а. Обозначим через с1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b1.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.