|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Задачи-1(7 класс)</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Задачи, прямые, точка, прямые, полупрямые, треугольник, угол, полуплоскости</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Задачи-1(7 класс)''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Задачи-1(7 класс)''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''ЗАДАЧИ'''<br> | + | '''Задачи'''<br> |
| | | | |
| | <br>1. 1) Проведите прямую. Отметьте какую-нибудь точку А, лежащую на прямой, и точку В, не лежащую на прямой. | | <br>1. 1) Проведите прямую. Отметьте какую-нибудь точку А, лежащую на прямой, и точку В, не лежащую на прямой. |
| | | | |
| - | 2) Проведите две пересекающиеся прямые а и b<br> | + | 2) Проведите две пересекающиеся '''[[Шпаргалки на тему «Паралельні та перпендикулярні прямі, їх властивості. Доведення від супротивного»|прямые]]''' а и b<br> |
| | | | |
| - | {| cellspacing="1" cellpadding="1" border="1" style="width: 584px; height: 200px;" | + | <br> |
| | + | |
| | + | {| cellspacing="1" cellpadding="1" border="1" style="width: 577px; height: 105px;" |
| | |- | | |- |
| - | | Многие задачи настоящего учебника взяты из школьных учебников и задачников прошлых лет, в особенности из «Геометрии» А. П. Киселева и «Сборника задач по геометрии» Н. А. Рыбкина. Число в прямоугольнике указывает на номер пункта, материал которого используется в решениях следующих за ним задач. | + | | |
| | + | Многие задачи настоящего учебника взяты из школьных учебников и задачников прошлых лет, в особенности из «Геометрии» А. П. Киселева и «Сборника задач по геометрии» Н. А. Рыбкина. Число в прямоугольнике указывает на номер пункта, материал которого используется в решениях следующих за ним задач. |
| | + | |
| | |} | | |} |
| | | | |
| - | <br>[[Image:20-06-60.jpg]]<br><br>Отметьте точку С пересечения прямых; точку А на прямой а, не лежащую на прямой b; точку В, не лежащую ни на одной из прямых a и b. | + | <br>[[Image:20-06-60.jpg|240px|Линейка]]<br><br>Отметьте точку С пересечения прямых; точку А на прямой а, не лежащую на прямой b; точку В, не лежащую ни на одной из прямых a и b. |
| | | | |
| | 2. Отметьте на листе бумаги две точки. Проведите через них от руки прямую. С помощью линейки проверьте правильность построения.<br> | | 2. Отметьте на листе бумаги две точки. Проведите через них от руки прямую. С помощью линейки проверьте правильность построения.<br> |
| | | | |
| - | 3. Могут ли две прямые иметь две точки пересечения? Объяните ответ.<br> | + | 3. Могут ли две прямые иметь две точки пересечения? Объясните ответ.<br> |
| | | | |
| - | 4. Для проверки правильности линейки применяют такой способ. Через две точки с помощью линейки проводят линию (рис. 27). Затем линейку переворачивают и через те же точки снова проводят линию. Если линии не совпадают, то линейка неправильная. На каком свойстве прямых основан этот способ проверки правильности линейки? | + | 4. Для проверки правильности линейки применяют такой способ. Через две точки с помощью линейки проводят линию (рис. 27). Затем линейку переворачивают и через те же точки снова проводят линию. Если линии не совпадают, то линейка неправильная. На каком свойстве прямых основан этот способ проверки правильности линейки? |
| | | | |
| - | 5. Проведите прямую а. Отметьте на прямой две какие-нибудь точки А Vi В. Отметьте теперь точку С так, чтобы точка А лежала между точками В м С. | + | 5. Проведите прямую а. Отметьте на прямой две какие-нибудь точки А и В. Отметьте теперь точку С так, чтобы '''[[Точки і прямі, їх властивості. Закриті вправи|точка]]''' А лежала между точками В м С. |
| | | | |
| | 6. Проведите прямую a. Отметьте на прямой две какие-нибудь точки А и В. Отметьте теперь какую-нибудь точку С отрезка АВ. | | 6. Проведите прямую a. Отметьте на прямой две какие-нибудь точки А и В. Отметьте теперь какую-нибудь точку С отрезка АВ. |
| Строка 36: |
Строка 40: |
| | 3) СМ =12,3 м, MD = 5,8 м. | | 3) СМ =12,3 м, MD = 5,8 м. |
| | | | |
| - | 8. Отметьте на прямой две точки. Отметьте на глаз середину отрезка, соединяющего эти точки. Проверьте правильность построения измерениями с помощью линейки. | + | 8. Отметьте на прямой две точки. Отметьте на глаз середину отрезка, соединяющего эти точки. Проверьте правильность построения измерениями с помощью линейки. |
| | | | |
| - | 9. Три точки А, В, С лежат на одной прямой. Известно, что АВ=4,3 см, АС = 7,5 см, ВС = 3,2 см. Может ли точка А лежать между точками В и С? Может ли точка С лежать между точками А и В? Какая из трех точек А, В, С лежит между двумя другими? | + | 9. Три точки А, В, С лежат на одной прямой. Известно, что АВ=4,3 см, АС = 7,5 см, ВС = 3,2 см. Может ли точка А лежать между точками В и С? Может ли точка С лежать между точками А и В? Какая из трех точек А, В, С лежит между двумя другими? |
| | | | |
| - | 10. Точки А, В, С лежат на одной прямой. Принадлежит ли точка В отрезку АС, если АС= 5 см, ВС = 7 см? Объясните ответ. | + | 10. Точки А, В, С лежат на одной прямой. Принадлежит ли точка В '''[[Измерение отрезков. Полные уроки|отрезку]]''' АС, если АС= 5 см, ВС = 7 см? Объясните ответ. |
| | | | |
| - | 11. Точки А, В, С лежат на одной прямой. Может ли точка В разделять точки А и С, если АС = 7 м, ВС = 7,6 м? Объясните ответ. | + | 11. Точки А, В, С лежат на одной прямой. Может ли точка В разделять точки А и С, если АС = 7 м, ВС = 7,6 м? Объясните ответ. |
| | | | |
| - | 12. Могут ли точки А, В, С лежать на одной прямой, если АВ=1,8 м, АС = 1,3 м, ВС = 3 м? Объясните ответ. | + | 12. Могут ли точки А, В, С лежать на одной прямой, если АВ=1,8 м, АС = 1,3 м, ВС = 3 м? Объясните ответ. |
| | | | |
| - | 13. Могут ли три точки А, В, С лежать на одной прямой, если длина большего отрезка АВ меньше суммы длин отрезков АС к ВС? Объясните ответ. | + | 13. Могут ли три точки А, В, С лежать на одной прямой, если длина большего отрезка АВ меньше суммы длин отрезков АС к ВС? Объясните ответ. |
| | | | |
| - | 14. Точки А, В, С лежат на одной прямой. Найдите длину отрезка ВС, если АВ = 2,7 т, АС = 3,2 м. Сколько решений имеет задача? | + | 14. Точки А, В, С лежат на одной прямой. Найдите длину отрезка ВС, если АВ = 2,7 т, АС = 3,2 м. Сколько решений имеет задача? |
| | | | |
| | 15. На отрезке АВ длиной 15 м отмечена точка С. Найдите длины отрезков АС и ВС, если: | | 15. На отрезке АВ длиной 15 м отмечена точка С. Найдите длины отрезков АС и ВС, если: |
| Строка 62: |
Строка 66: |
| | 16. Проведите прямую и отметьте какую-нибудь точку А, не лежащую на этой прямой. Отметьте теперь две точки В иС так, чтобы отрезок АВ пересекал прямую, а отрезок ВС не пересекал ее. | | 16. Проведите прямую и отметьте какую-нибудь точку А, не лежащую на этой прямой. Отметьте теперь две точки В иС так, чтобы отрезок АВ пересекал прямую, а отрезок ВС не пересекал ее. |
| | | | |
| - | 17. Даны прямая и три точки А, В, С, не лежащие на этой прямой. Известно, что отрезок АВ пересекает прямую, а отрезок АС не пересекает ее. Пересекает ли прямую отрезок ВС? Объясните ответ. | + | 17. Даны прямая и три точки А, В, С, не лежащие на этой прямой. Известно, что отрезок АВ пересекает прямую, а отрезок АС не пересекает ее. Пересекает ли прямую отрезок ВС? Объясните ответ. |
| | | | |
| - | 18. Даны прямая и четыре точки А, В, С и D, не лежащие на этой прямой. Пересекает ли прямую отрезок AD, если: | + | 18. Даны прямая и четыре точки А, В, С и D, не лежащие на этой прямой. Пересекает ли прямую отрезок AD, если: |
| | | | |
| | 1) отрезки АВ, ВС и CD пересекают прямую; | | 1) отрезки АВ, ВС и CD пересекают прямую; |
| Строка 78: |
Строка 82: |
| | 6) отрезки АС, ВС и BD пересекают прямую? Объясните ответ. | | 6) отрезки АС, ВС и BD пересекают прямую? Объясните ответ. |
| | | | |
| - | 19. Даны пять точек и прямая, не проходящая ни через одну из этих точек. Известно, что три точки расположены в одной полуплоскости относительно этой прямой, а две точки — в другой. Каждая пара точек соединена отрезком. Сколько отрезков пересекает прямую? Объясните ответ. | + | 19. Даны пять точек и прямая, не проходящая ни через одну из этих точек. Известно, что три точки расположены в одной '''[[Полуплоскости|полуплоскости]]''' относительно этой прямой, а две точки — в другой. Каждая пара точек соединена отрезком. Сколько отрезков пересекает прямую? Объясните ответ. |
| | | | |
| | 20. Даны прямая а и точки А, X, Y, Z на этой прямой (рис. 11). Известно, что точки X и У лежат по одну сторону от точки А, точки X и Z тоже лежат по одну сторону от точки А. Как расположены точки Y w. Z относительно точки А: по одну сторону или по разные стороны? Объясните ответ. | | 20. Даны прямая а и точки А, X, Y, Z на этой прямой (рис. 11). Известно, что точки X и У лежат по одну сторону от точки А, точки X и Z тоже лежат по одну сторону от точки А. Как расположены точки Y w. Z относительно точки А: по одну сторону или по разные стороны? Объясните ответ. |
| | | | |
| - | 21. Отметьте две точки А к В. Проведите полупрямую АВ. | + | 21. Отметьте две точки А к В. Проведите полупрямую АВ. |
| | | | |
| - | 22. На отрезке АВ взята точка С. Среди полупрямых АВ, АС,СА, СВ назовите пары совпадающих полупрямых, дополнительных полупрямых. Объясните ответ. | + | 22. На отрезке АВ взята точка С. Среди полупрямых АВ, АС,СА, СВ назовите пары совпадающих полупрямых, дополнительных полупрямых. Объясните ответ. |
| | | | |
| | 23. Проведите из одной точки три произвольных луча. Определите на глаз углы, образуемые этими лучами. Проверьте ваши ответы, измеряя углы транспортиром. Повторите упражнение.<br> | | 23. Проведите из одной точки три произвольных луча. Определите на глаз углы, образуемые этими лучами. Проверьте ваши ответы, измеряя углы транспортиром. Повторите упражнение.<br> |
| Строка 90: |
Строка 94: |
| | 24. Луч а проходит между сторонами угла (cd). Найдите угол (cd), если:<br> | | 24. Луч а проходит между сторонами угла (cd). Найдите угол (cd), если:<br> |
| | | | |
| - | 1) [[Image:20-06-61.jpg]](aс) = 35°, [[Image:20-06-61.jpg]](ad) = 75°;<br> | + | 1) [[Image:20-06-61.jpg|Угол]](aс) = 35°, [[Image:20-06-61.jpg|Угол]](ad) = 75°;<br> |
| | | | |
| - | 2) [[Image:20-06-61.jpg]](ac)=57°, [[Image:20-06-61.jpg]](ad) = 62°; <br> | + | 2) [[Image:20-06-61.jpg|Угол]](ac)=57°, [[Image:20-06-61.jpg|Угол]](ad) = 62°; <br> |
| | | | |
| - | 3) [[Image:20-06-61.jpg]](aс) = 94°, [[Image:20-06-61.jpg]](ad) = 85°.<br> | + | 3) [[Image:20-06-61.jpg|Угол]](aс) = 94°, [[Image:20-06-61.jpg|Угол]](ad) = 85°.<br> |
| | | | |
| - | 25. Может ли луч с проходить между сторонами угла (ac),если: <br> | + | 25. Может ли луч с проходить между сторонами угла (ac),если: <br> |
| | | | |
| - | 1) [[Image:20-06-61.jpg]](ac) = 30°, [[Image:20-06-61.jpg]](cb) = 80°, [[Image:20-06-61.jpg]](ab) = 50°;<br> | + | 1) [[Image:20-06-61.jpg|Угол]](ac) = 30°, [[Image:20-06-61.jpg|Угол]](cb) = 80°, [[Image:20-06-61.jpg|Угол]](ab) = 50°;<br> |
| | | | |
| - | 2) [[Image:20-06-61.jpg]](ac) = 100°, [[Image:20-06-61.jpg]](cb)=90°;<br> | + | 2) [[Image:20-06-61.jpg|Угол]](ac) = 100°, [[Image:20-06-61.jpg|Угол]](cb)=90°;<br> |
| | | | |
| | 3) угол (ас) больше угла (аb)?<br> | | 3) угол (ас) больше угла (аb)?<br> |
| | | | |
| - | 26. Между сторонами угла (сb), равного 60°, проходит луч с.Найдите углы (ас) и (bс), если:<br> | + | 26. Между сторонами угла (сb), равного 60°, проходит луч с.Найдите углы (ас) и (bс), если:<br> |
| | | | |
| - | 1) угол (ас) на 30° больше угла (bс); <br> | + | 1) '''[[Практикум на тему «Суміжні кути, їх властивості»|Угол]]''' (ас) на 30° больше угла (bс); <br> |
| | | | |
| | 2) угол (ас) в два раза больше угла (bс);<br> | | 2) угол (ас) в два раза больше угла (bс);<br> |
| Строка 118: |
Строка 122: |
| | 1) АВ = 3 см; 2) АВ = 7 см; 3) АВ = 10 см.<br> | | 1) АВ = 3 см; 2) АВ = 7 см; 3) АВ = 10 см.<br> |
| | | | |
| - | 28. Постройте на глаз углы 30°, 45°, 60°, 90°. Проверьте точность построения транспортиром. Повторите задание.<br> | + | 28. Постройте на глаз углы 30°, 45°, 60°, 90°. Проверьте точность построения транспортиром. Повторите задание.<br> |
| | | | |
| - | 29. Существует ли на полупрямой АВ такая точка X, отличная от В, что АХ=АВ? Объясните ответ.<br> | + | 29. Существует ли на полупрямой АВ такая точка X, отличная от В, что АХ=АВ? Объясните ответ.<br> |
| | | | |
| - | 30. На луче АВ отложен отрезок АС, меньший отрезка АВ. Какая из трех точек А, В, С лежит между двумя другими? Объясните ответ.<br> | + | 30. На луче АВ отложен отрезок АС, меньший отрезка АВ. Какая из трех точек А, В, С лежит между двумя другими? Объясните ответ.<br> |
| | | | |
| - | 31. На луче АВ отмечена точка С. Найдите длину отрезка ВС, если: <br> | + | 31. На луче АВ отмечена точка С. Найдите длину отрезка ВС, если: <br> |
| | | | |
| | 1) АВ = 1,5 м, АС = 0,3 м; 2) АВ=2 см, АС = 4,4 см.<br> | | 1) АВ = 1,5 м, АС = 0,3 м; 2) АВ=2 см, АС = 4,4 см.<br> |
| Строка 130: |
Строка 134: |
| | 32. Постройте на глаз треугольник с равными сторонами (равносторонний треугольник). Проверьте точность построения измерением сторон.<br> | | 32. Постройте на глаз треугольник с равными сторонами (равносторонний треугольник). Проверьте точность построения измерением сторон.<br> |
| | | | |
| - | 33. На стороне АВ треугольника ABC взята точка D. Чему равна сторона АВ треугольника, если AD=5 см, а BD=6 см?<br> | + | 33. На стороне АВ треугольника ABC взята точка D. Чему равна сторона АВ треугольника, если AD=5 см, а BD=6 см?<br> |
| | | | |
| - | 34. На стороне АВ треугольника ABC взята точка D. Найдите угол С треугольника, если [[Image:20-06-61.jpg]]ACD = 30°, а [[Image:20-06-61.jpg]]BCD = 70°. | + | 34. На стороне АВ треугольника ABC взята точка D. Найдите угол С треугольника, если [[Image:20-06-61.jpg|Угол]]ACD = 30°, а [[Image:20-06-61.jpg|Угол]]BCD = 70°. |
| | | | |
| - | 35. Начертите какой-нибудь треугольник. Постройте от руки на глаз равный ему треугольник. Проверьте правильность построения, измеряя соответствующие углы и стороны. Повторите упражнение. | + | 35. Начертите какой-нибудь треугольник. Постройте от руки на глаз равный ему треугольник. Проверьте правильность построения, измеряя соответствующие углы и стороны. Повторите упражнение. |
| | | | |
| - | 36. Треугольники ABC и PQR равны. Известно, что АВ=5 см, ВС=6 см, АС = 7 см. Найдите стороны треугольника PQR. Объясните ответ. | + | 36. Треугольники ABC и PQR равны. Известно, что АВ=5 см, ВС=6 см, АС = 7 см. Найдите стороны треугольника PQR. Объясните ответ. |
| | | | |
| - | 37. Треугольники ABC и PQR равны. Углы второго треугольника известны: [[Image:20-06-61.jpg]]Р = 40°, [[Image:20-06-61.jpg]]Q = 60°, [[Image:20-06-61.jpg]]R = 80°. Найдите углы треугольника ABC. | + | 37. Треугольники ABC и PQR равны. Углы второго треугольника известны: [[Image:20-06-61.jpg|Угол]]Р = 40°, [[Image:20-06-61.jpg|Угол]]Q = 60°, [[Image:20-06-61.jpg|Угол]]R = 80°. Найдите углы треугольника ABC. |
| | | | |
| - | 38. Треугольники ABC и PQR равны. Известно, что сторона АВ равна 10 м, а угол С равен 90°. Чему равны сторона PQ и угол R? Объясните ответ. | + | 38. Треугольники ABC и PQR равны. Известно, что сторона АВ равна 10 м, а угол С равен 90°. Чему равны сторона PQ и угол R? Объясните ответ. |
| | | | |
| - | 39. Треугольники ABC, PQR и XYZ равны. Известно, что АВ = 5 см, QR = 6 см, ZX = 1 см. Найдите остальные стороны каждого треугольника. | + | 39. '''[[Презентація уроку на тему «Трикутник і його елементи»|Треугольники]]''' ABC, PQR и XYZ равны. Известно, что АВ = 5 см, QR = 6 см, ZX = 1 см. Найдите остальные стороны каждого треугольника. |
| | | | |
| - | 40. Дан треугольник ABC. Существует ли другой, равный ему треугольник ABD? | + | 40. Дан треугольник ABC. Существует ли другой, равный ему треугольник ABD? |
| | | | |
| - | 41. Может ли прямая, пересекающая одну из двух параллельных прямых, не пересекать другую? Объясните ответ. | + | 41. Может ли прямая, пересекающая одну из двух параллельных прямых, не пересекать другую? Объясните ответ. |
| | | | |
| - | 42. Даны две пересекающиеся прямые. Можно ли провести третью прямую, параллельную каждой из двух данных? | + | 42. Даны две пересекающиеся прямые. Можно ли провести третью прямую, параллельную каждой из двух данных? |
| | | | |
| | 43. Может ли прямая, не проходящая ни через одну из вершин треугольника, пересекать каждую его сторону? Почему? | | 43. Может ли прямая, не проходящая ни через одну из вершин треугольника, пересекать каждую его сторону? Почему? |
| Строка 164: |
Строка 168: |
| | 1) отрезок АС с концами на сторонах угла; | | 1) отрезок АС с концами на сторонах угла; |
| | | | |
| - | 2) любой отрезок CD с концами на сторонах угла (рис. 30).<br> <br><br> [[Image:20-06-63.jpg]]<br><br> <br>50. Докажите, что две прямые либо параллельны, либо пересекаются в одной точке. | + | 2) любой отрезок CD с концами на сторонах угла (рис. 30).<br> <br><br> [[Image:20-06-63.jpg|550px|20-06-63.jpg]]<br><br> <br>50. Докажите, что две прямые либо параллельны, либо пересекаются в одной точке. |
| | | | |
| | 51*. Точки А и С принадлежат прямой а. На полупрямой С А отложен отрезок СВ, больший отрезка С А. | | 51*. Точки А и С принадлежат прямой а. На полупрямой С А отложен отрезок СВ, больший отрезка С А. |
| Строка 170: |
Строка 174: |
| | 1) Какая из трех точек А, В, С лежит между двумя другими? Объясните ответ. | | 1) Какая из трех точек А, В, С лежит между двумя другими? Объясните ответ. |
| | | | |
| - | 2) Докажите, что точка А разбивает прямую а на две полуйрямые АВ к АС. <br> | + | 2) Докажите, что точка А разбивает прямую а на две '''[[Полупрямая|полупрямые]]''' АВ к АС. <br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | <sub>Книги и учебники согласно календарному плануванння по математике 7 класса [[Математика|скачать]], помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | + | <br> <br> <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 20:32, 15 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Задачи-1(7 класс)
Задачи
1. 1) Проведите прямую. Отметьте какую-нибудь точку А, лежащую на прямой, и точку В, не лежащую на прямой.
2) Проведите две пересекающиеся прямые а и b
|
Многие задачи настоящего учебника взяты из школьных учебников и задачников прошлых лет, в особенности из «Геометрии» А. П. Киселева и «Сборника задач по геометрии» Н. А. Рыбкина. Число в прямоугольнике указывает на номер пункта, материал которого используется в решениях следующих за ним задач.
|
Отметьте точку С пересечения прямых; точку А на прямой а, не лежащую на прямой b; точку В, не лежащую ни на одной из прямых a и b.
2. Отметьте на листе бумаги две точки. Проведите через них от руки прямую. С помощью линейки проверьте правильность построения.
3. Могут ли две прямые иметь две точки пересечения? Объясните ответ.
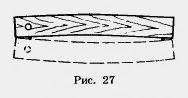
4. Для проверки правильности линейки применяют такой способ. Через две точки с помощью линейки проводят линию (рис. 27). Затем линейку переворачивают и через те же точки снова проводят линию. Если линии не совпадают, то линейка неправильная. На каком свойстве прямых основан этот способ проверки правильности линейки?
5. Проведите прямую а. Отметьте на прямой две какие-нибудь точки А и В. Отметьте теперь точку С так, чтобы точка А лежала между точками В м С.
6. Проведите прямую a. Отметьте на прямой две какие-нибудь точки А и В. Отметьте теперь какую-нибудь точку С отрезка АВ.
7. Точка М лежит на прямой CD между точками С и D. Найдите длину отрезка CD, если:
1) СМ=2,5 см, MD = 3,5 см;
2) СМ=3,1 дм, MD = 4,6 дм;
3) СМ =12,3 м, MD = 5,8 м.
8. Отметьте на прямой две точки. Отметьте на глаз середину отрезка, соединяющего эти точки. Проверьте правильность построения измерениями с помощью линейки.
9. Три точки А, В, С лежат на одной прямой. Известно, что АВ=4,3 см, АС = 7,5 см, ВС = 3,2 см. Может ли точка А лежать между точками В и С? Может ли точка С лежать между точками А и В? Какая из трех точек А, В, С лежит между двумя другими?
10. Точки А, В, С лежат на одной прямой. Принадлежит ли точка В отрезку АС, если АС= 5 см, ВС = 7 см? Объясните ответ.
11. Точки А, В, С лежат на одной прямой. Может ли точка В разделять точки А и С, если АС = 7 м, ВС = 7,6 м? Объясните ответ.
12. Могут ли точки А, В, С лежать на одной прямой, если АВ=1,8 м, АС = 1,3 м, ВС = 3 м? Объясните ответ.
13. Могут ли три точки А, В, С лежать на одной прямой, если длина большего отрезка АВ меньше суммы длин отрезков АС к ВС? Объясните ответ.
14. Точки А, В, С лежат на одной прямой. Найдите длину отрезка ВС, если АВ = 2,7 т, АС = 3,2 м. Сколько решений имеет задача?
15. На отрезке АВ длиной 15 м отмечена точка С. Найдите длины отрезков АС и ВС, если:
1) отрезок АС на 3 м длиннее отрезка ВС;
2) отрезок АС в два раза длиннее отрезка ВС;
3) точка С — середина отрезка АВ;
4) длины отрезков АС и ВС относятся как 2:3.
16. Проведите прямую и отметьте какую-нибудь точку А, не лежащую на этой прямой. Отметьте теперь две точки В иС так, чтобы отрезок АВ пересекал прямую, а отрезок ВС не пересекал ее.
17. Даны прямая и три точки А, В, С, не лежащие на этой прямой. Известно, что отрезок АВ пересекает прямую, а отрезок АС не пересекает ее. Пересекает ли прямую отрезок ВС? Объясните ответ.
18. Даны прямая и четыре точки А, В, С и D, не лежащие на этой прямой. Пересекает ли прямую отрезок AD, если:
1) отрезки АВ, ВС и CD пересекают прямую;
2) отрезки АС и ВС пересекают прямую, а отрезок BD не пересекает;
3) отрезки АВ и CD пересекают прямую, а отрезок ВС не пересекает;
4) отрезки АВ и CD не пересекают прямую, а отрезок ВС пересекает;
5) отрезки АВ, ВС, CD не пересекают прямую;
6) отрезки АС, ВС и BD пересекают прямую? Объясните ответ.
19. Даны пять точек и прямая, не проходящая ни через одну из этих точек. Известно, что три точки расположены в одной полуплоскости относительно этой прямой, а две точки — в другой. Каждая пара точек соединена отрезком. Сколько отрезков пересекает прямую? Объясните ответ.
20. Даны прямая а и точки А, X, Y, Z на этой прямой (рис. 11). Известно, что точки X и У лежат по одну сторону от точки А, точки X и Z тоже лежат по одну сторону от точки А. Как расположены точки Y w. Z относительно точки А: по одну сторону или по разные стороны? Объясните ответ.
21. Отметьте две точки А к В. Проведите полупрямую АВ.
22. На отрезке АВ взята точка С. Среди полупрямых АВ, АС,СА, СВ назовите пары совпадающих полупрямых, дополнительных полупрямых. Объясните ответ.
23. Проведите из одной точки три произвольных луча. Определите на глаз углы, образуемые этими лучами. Проверьте ваши ответы, измеряя углы транспортиром. Повторите упражнение.
24. Луч а проходит между сторонами угла (cd). Найдите угол (cd), если:
1)  (aс) = 35°, (aс) = 35°,  (ad) = 75°; (ad) = 75°;
2)  (ac)=57°, (ac)=57°,  (ad) = 62°; (ad) = 62°;
3)  (aс) = 94°, (aс) = 94°,  (ad) = 85°. (ad) = 85°.
25. Может ли луч с проходить между сторонами угла (ac),если:
1)  (ac) = 30°, (ac) = 30°,  (cb) = 80°, (cb) = 80°,  (ab) = 50°; (ab) = 50°;
2)  (ac) = 100°, (ac) = 100°,  (cb)=90°; (cb)=90°;
3) угол (ас) больше угла (аb)?
26. Между сторонами угла (сb), равного 60°, проходит луч с.Найдите углы (ас) и (bс), если:
1) Угол (ас) на 30° больше угла (bс);
2) угол (ас) в два раза больше угла (bс);
3) луч с делит угол (аb) пополам;
4) градусные меры углов (ас) и (bс)
относятся как 2:3.
27. Проведите прямую. Отметьте на ней какую-нибудь точку А. Затем отметьте на глаз точку В этой прямой так, чтобы АВ=5 см. Проверьте точность построения точки В линейкой. Повторите упражнение для:
1) АВ = 3 см; 2) АВ = 7 см; 3) АВ = 10 см.
28. Постройте на глаз углы 30°, 45°, 60°, 90°. Проверьте точность построения транспортиром. Повторите задание.
29. Существует ли на полупрямой АВ такая точка X, отличная от В, что АХ=АВ? Объясните ответ.
30. На луче АВ отложен отрезок АС, меньший отрезка АВ. Какая из трех точек А, В, С лежит между двумя другими? Объясните ответ.
31. На луче АВ отмечена точка С. Найдите длину отрезка ВС, если:
1) АВ = 1,5 м, АС = 0,3 м; 2) АВ=2 см, АС = 4,4 см.
32. Постройте на глаз треугольник с равными сторонами (равносторонний треугольник). Проверьте точность построения измерением сторон.
33. На стороне АВ треугольника ABC взята точка D. Чему равна сторона АВ треугольника, если AD=5 см, а BD=6 см?
34. На стороне АВ треугольника ABC взята точка D. Найдите угол С треугольника, если  ACD = 30°, а ACD = 30°, а  BCD = 70°. BCD = 70°.
35. Начертите какой-нибудь треугольник. Постройте от руки на глаз равный ему треугольник. Проверьте правильность построения, измеряя соответствующие углы и стороны. Повторите упражнение.
36. Треугольники ABC и PQR равны. Известно, что АВ=5 см, ВС=6 см, АС = 7 см. Найдите стороны треугольника PQR. Объясните ответ.
37. Треугольники ABC и PQR равны. Углы второго треугольника известны:  Р = 40°, Р = 40°,  Q = 60°, Q = 60°,  R = 80°. Найдите углы треугольника ABC. R = 80°. Найдите углы треугольника ABC.
38. Треугольники ABC и PQR равны. Известно, что сторона АВ равна 10 м, а угол С равен 90°. Чему равны сторона PQ и угол R? Объясните ответ.
39. Треугольники ABC, PQR и XYZ равны. Известно, что АВ = 5 см, QR = 6 см, ZX = 1 см. Найдите остальные стороны каждого треугольника.
40. Дан треугольник ABC. Существует ли другой, равный ему треугольник ABD?
41. Может ли прямая, пересекающая одну из двух параллельных прямых, не пересекать другую? Объясните ответ.
42. Даны две пересекающиеся прямые. Можно ли провести третью прямую, параллельную каждой из двух данных?
43. Может ли прямая, не проходящая ни через одну из вершин треугольника, пересекать каждую его сторону? Почему?
44*. Даны четыре точки А, В, С и D. Известно, что точки А, В, С лежат на одной прямой и точки В, С, D также лежат на одной прямой. Докажите, что все четыре точки лежат на одной прямой.
45.* Даны четыре прямые а, b, с и d. Известно, что прямые a, b, с пересекаются в одной точке и прямые b, с, d также пересекаются в одной точке. Докажите, что все четыре данные прямые проходят через одну точку. Точки А, В, С, D не лежат на одной прямой. Известно, что прямая АВ пересекает отрезок CD, а прямая CD пересекает отрезок АВ. Докажите, что отрезки АВ и CD пересекаются.
46*.Дан треугольник ABC. На стороне АС взята точка В1, а на стороне ВС — точка А1. Докажите, что отрезки АА1 и BB1 пересекаются (рис. 28).
47*. Отрезки АВ и CD, не лежащие на одной прямой, пересекаются в точке Е. Докажите, что отрезок АС не пересекает прямую BD (рис. 29).
49*. Докажите, что если луч, исходящий из вершины угла, пересекает отрезок АВ с концами на сторонах угла, то он пересекает:
1) отрезок АС с концами на сторонах угла;
2) любой отрезок CD с концами на сторонах угла (рис. 30).
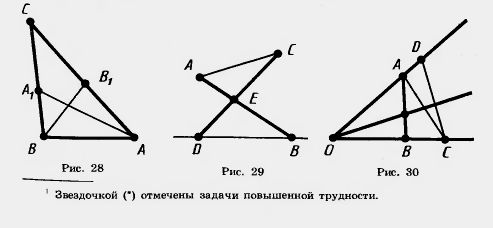
50. Докажите, что две прямые либо параллельны, либо пересекаются в одной точке.
51*. Точки А и С принадлежат прямой а. На полупрямой С А отложен отрезок СВ, больший отрезка С А.
1) Какая из трех точек А, В, С лежит между двумя другими? Объясните ответ.
2) Докажите, что точка А разбивает прямую а на две полупрямые АВ к АС.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|












