|
Гипермаркет знаний>>Черчение 9 класс>>Черчение: Чертежи в системе прямоугольных проекций
Вы научились строить аксонометрические изображения, в основу которых положено параллельное проецирование. С помощью параллельного проецирования можно построить и другие изображения. Наиболее широко применяемыми в технике являются изображения, которые получены при прямоугольном проецировании на одну, две и три взаимно перпендикулярные плоскости проекций.
Проекция точки на плоскость
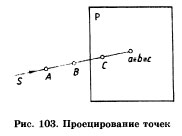
Вывод: Рассмотрим другой пример. На проецирующем луче разместим три точки: А, В, С (рис. 103). Их проекцией на плоскости Р является точка а, следовательно, а=Ь=c. По одной проекции нельзя определить, сколько объектов (точек) было на нее спроецировано.
Прямоугольное (ортогональное) проецирование точки на две плоскости проекций. Метод выполнения прямоугольных изображений на две взаимно перпендикулярные плоскости проекций впервые был разработан в 1799 году французским инженером и ученым Гаспаром Монжем, который считается основоположником начертательной геометрии — науки об изображении предметов и графических способах решения задач.
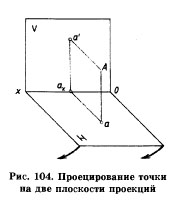
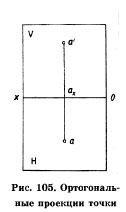
Для того чтобы получить две проекции точки, определяющих положение ее в пространстве, возьмем две взаимно перпендикулярные плоскости: V — фронтальную и Н — горизонтальную. Они будут пересекаться по прямой ох, которую называют осью проекций (рис. 104). Расположим точку А в двугранном углу. Используя метод прямоугольного проецирования, спроецируем ее на плоскости проекций, получим фронтальную (а') и горизонтальную (а) проекции точки А. Запись а' читается как «а штрих». Мы рассмотрели метод получения изображений точки А в системе двух плоскостей проекций. Чтобы решить обратную задачу: по изображениям точки найти ее положение в пространстве, необходимо от проекций а и а' провести проецирующие лучи перпендикулярно плоскостям проекций. Их пересечение определит положение точки А в пространстве. Повернем плоскость Н вокруг оси ОХ на 90° вниз, до совмещения с плоскостью V, как показано на рис. 105. Получим ортогональные проекции точки. Обратите внимание на то, что проекции а и а' расположились на одной прямой а'а (рис. 105). Линия аа' называется линией проекционной связи.
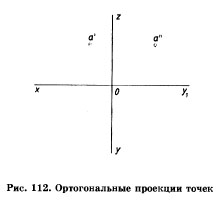
Прямоугольное (ортогональное) проецирование точки на три плоскости проекций
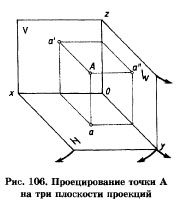
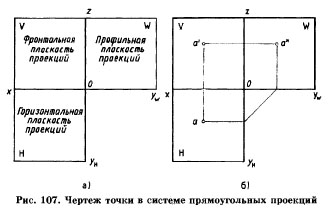
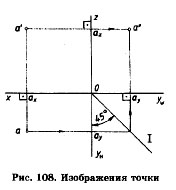
Плоскости проекций Н и W разворачивают до совмещения с плоскостью V, как показано на рис. 106, 107. Линии пересечения плоскостей являются осями проекций ох, оу, ох (рис. 106). Обратим внимание на то, что проекции а' и а, а' и а", а и а" лежат на прямых, называемых линиями проекционной связи (рис. 107). Такая зависимость в расположении проекций точки называется проекционной связью и при выполнении чертежей должна обязательно соблюдаться. Чертеж, состоящий из нескольких прямоугольных проекций, называется чертежом в системе прямоугольных проекций, или ортогональным чертежом.
Чертеж точки в системе прямоугольных проекций представлен на рис. 107, б.Построение третьей проекции точки по двум заданным.
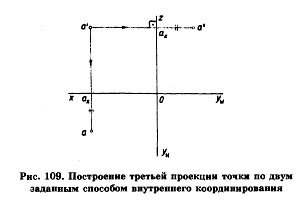
Профильную проекцию а" точки А можно найти способом координирования, показанным на рис. 109. Из точки а' проведем линию проекционной связи к оси z, на ней отложим отрезок aza" = аха. Обратите внимание на то, что расстояние от оси z до профильной проекции точки равно расстоянию от оси х до ее горизонтальной проекции.
Вопросы и задания Ортогональный чертеж
6. Какие плоскости проекций вы знаете? Как они обозначаются?
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: