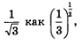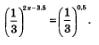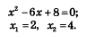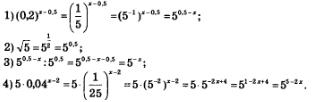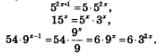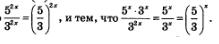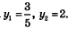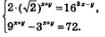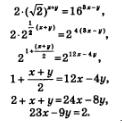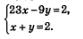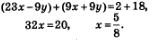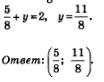|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Показательные уравнения
§ 46. Показательные уравнения
Показательными уравнениями называют уравнения вида
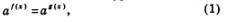
где а — положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.
Опираясь на полученные в предыдущем параграфе теоремы 1 и 3, согласно которым равенство 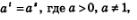 , справедливо тогда и только тогда, когда t =s, мы можем сформулировать следующее утверждение. , справедливо тогда и только тогда, когда t =s, мы можем сформулировать следующее утверждение.
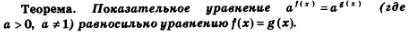
Пример 1. Решить уравнения:
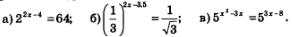
Решение. а) Представив 64 как 26 , перепишем заданное уравнение в виде 22x-4 =26. Это уравнение равносильно уравнению 2x -4=6, откуда находим: х = 5.
б) Представив 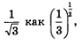 перепишем заданное уравнение в виде перепишем заданное уравнение в виде 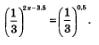
Это уравнение равносильно уравнению 2x - 3,5 = 0,5, откуда находим: х = 2
в) Заданное уравнение равносильно уравнению х2 - Зx = Зx-8. Далее имеем:
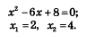
Пример 2. Решить уравнение: 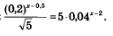
Решение. Здесь есть возможность и левую, и правую части уравнения представить в виде степени с основанием 5. В самом деле:
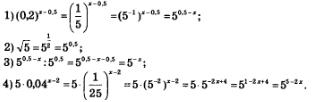
Таким образом, заданное уравнение мы преобразовали к виду: 5~х=5-2х.
Далее получаем:x = 5-2 x и, следовательно, x = 5.
Пример 3. Решить уравнение: 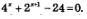
Решение. Заметив, что 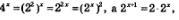 перепишем заданное уравнение в виде: перепишем заданное уравнение в виде:
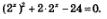
Есть смысл ввести новую переменную у = 2х; тогда уравнение примет вид: у2 + 2у -24 = 0. Решив квадратное уравнение относительно у, находим у1 =4, у2 =-6. Но у = 2x, значит, нам остается решить два уравнения:
2х =4; 2х =-6.
Из первого уравнения находим x = 2, а второе уравнение не имеет корней, поскольку при любых значениях х выполняется неравенство 2х >0.
Ответ: х = 2.
Подведем некоторые итоги. Можно выделить три основных метода решения показательных уравнений:
1) Функционально-графическийметод. Он основан на использовании графических иллюстраций или каких-либо свойств функций. Мы применяли этот метод в § 45.
2) Метод уравнивания показателей. Он основан на теореме о том, что уравнение 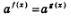 равносильно уравнению f(х) = g(х), где a — положительное число, отличное от 1. Мы применили этот метод в примерах 1 и 2. равносильно уравнению f(х) = g(х), где a — положительное число, отличное от 1. Мы применили этот метод в примерах 1 и 2.
3) Метод введения новой переменной. Мы применили этот метод в примере 3.
Рассмотрим более сложный пример, в котором для решения показательного уравнения используется метод введения новой переменной, и пример решения системы показательных уравнений.
Пример 4. Решить уравнение:
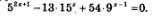
Решение. Воспользуемся тем, что
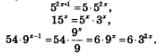
Это позволяет переписать заданное уравнение в более удобном виде:
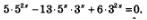
Разделив обе части уравнения почленно на З2x, получим равносильное ему уравнение:
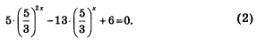
Мы воспользовались тем, что 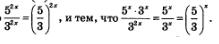
Теперь, как видите, «проявилась» новая переменная: 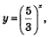 ,относительно которой уравнение (2) имеет вид квадратного уравнения: ,относительно которой уравнение (2) имеет вид квадратного уравнения:
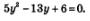
Корнями этого уравнения служат числа 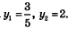 Значит, нам остается решить два уравнения: Значит, нам остается решить два уравнения:
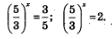
С первым из этих уравнений проблем нет:
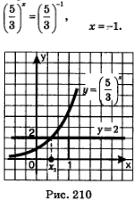
Со вторым уравнением у нас возникает проблема: как представить число 2 в виде некоторой степени числа 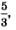 мы пока не знаем. Между тем второе уравнение тоже имеет единственный корень — это хорошо видно из графической иллюстрации, представленной на рис. 210. Придется нам в дальнейшем еще раз вернуться к этому уравнению. мы пока не знаем. Между тем второе уравнение тоже имеет единственный корень — это хорошо видно из графической иллюстрации, представленной на рис. 210. Придется нам в дальнейшем еще раз вернуться к этому уравнению.
Ответ: х1 =-1, х2 — корень уравнения 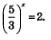
Пример 5. Решить систему уравнений:
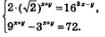
Решение. 1) Преобразуем первое уравнение системы к более простому виду:
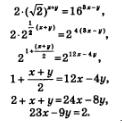
2) Преобразуем второе уравнение системы к более простому виду. Введем новую переменную 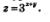 Тогда второе уравнение системы примет вид: z2 - z = 72, откуда находим:z1 =9, z2 = -8. Тогда второе уравнение системы примет вид: z2 - z = 72, откуда находим:z1 =9, z2 = -8.
Из уравнения 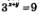 находим х + у = 2; уравнение находим х + у = 2; уравнение 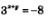 не имеет решений. не имеет решений.
Итак, второе уравнение системы нам удалось преобразовать к виду: х + у = 2.
3) Решим полученную систему уравнений:
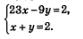
Умножим обе части второго уравнения на 9 и сложим полученное уравнение с первым уравнением системы:
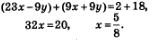
Из уравнения х + у = 2 находим:
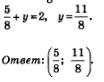
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|