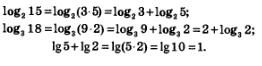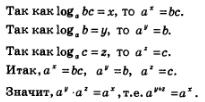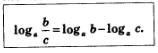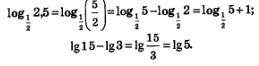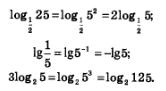|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Свойства логарифмов
Свойства логарифмов
B предыдущих параграфах мы ввели понятие логарифма положительного числа по положительному и отличному от 1 основанию, изучили свойства функции у=logax, построили ее график. Но, чтобы успешно использовать на практике операцию логарифмирования, нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе. Все свойства формулируются и доказываются только для положительных значений переменных, содержащихся под знаками логарифмов. Впрочем, два свойства доказательства не требуют, они представляют собой запись на математическом языке определения логарифма как показателя степени, мы ими уже пользовались:
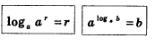
Теорема 1. Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел:
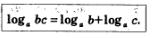
Например,
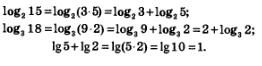
Доказательство. Введем следующие обозначения:
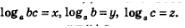 . .
Нам надо доказать, что выполняется равенство х = у+z.
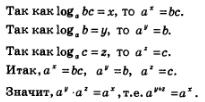
Но если степени двух положительных чисел равны и основания степеней равны и отличны от 1, то равны и показатели степеней: у+z = х, что и требовалось доказать.
Приведем краткую запись доказательства теоремы.

Замечания: 1. Математики считают, что теорему 1 можно не доказывать. Ведь что такое логарифм, спрашивают они. И отвечают: логарифм — это показатель степени. А что делается с показателями степеней при умножении? Они складываются. Значит, логарифм произведения равен сумме логарифмов. Вот в чем состоит содержательный смысл теоремы 1.
2. Теорема остается справедливой и для случая, когда логарифмируемое выражение представляет собой произведение более двух положительных чисел.
Например,
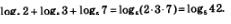
3. Теорему 1 можно сформулировать, используя конструкцию «если.. .то» (как принято для теорем в математике). Приведем соответствующую формулировку: если а,Ь и с — положительные числа, причем 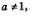 то справедливо равенство то справедливо равенство
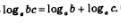 . .
Следующую теорему мы именно так и оформим.
Теорема 2. Если а,b с — положительные числа, причем 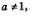 , то справедливо равенство: , то справедливо равенство:
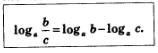
Краткая формулировка, которую удобнее использовать на практике: логарифм частного равен разности логарифмов делимого и делителя или логарифм дроби равен разности логарифмов числителя и знаменателя.
Например,
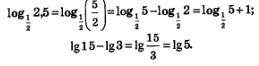
Доказательство. Мы приведем краткую запись доказательства, а вы попробуйте сделать соответствующие комментарии, аналогичные тем, что были приведены при доказательстве теоремы 1, а также дать содержательное истолкование теоремы 2 подобно тому, как это сделано в замечании 1.

Подготовка к доказательству (введение новых переменных) Перевод на более простой язык Доказательство
Теорема 3. Если а,Ь — положительные числа, причем 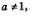 , то для любого числа г справедливо равенство: , то для любого числа г справедливо равенство:
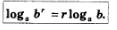
Краткая формулировка, которую удобнее использовать на практике: логарифм степени равен произведению показателя степени на логарифм основания степени.
Например,
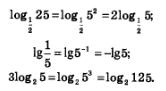
Доказательство. Приведем краткую запись доказательства, а вы, как и при доказательстве теоремы 2, попробуйте сделать соответствующие комментарии по аналогии с теоремой 1 и замечанием 1.

А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|