Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика:Признаки делимости на 10, на 5 и на 2

2. Признаки делимости на 10, на 5 и на 2

Всякое натуральное число, запись которого оканчивается цифрой 0, делится без остатка на 10. Чтобы получить частное, достаточно отбросить эту цифру 0. Например, 280 делится без остатка на 10, так как 280:10 = 28.

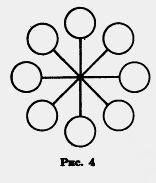
При делении же числа 283 на 10 получаем неполное частное 28 и остаток 3 (т. е. последнюю цифру записи этого числа). Поэтому если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10.

Если запись натурального числа оканчивается цифрой О, то это число делится без остатка на 10. Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре.

Число 10 = 2 «5. Поэтому число 10 делится без остатка и на 2, и на 5. Отсюда и любое число, запись которого оканчивается цифрой 0, делится без остатка и на 5, и на 2.

Например, 60=6.10 = 6.(2.5) = (6.2).5 = 12.5, значит, 60:5 = 12. А из того, что 60=6.(5.2)=(6.5).2 = 30.2, получаем, что 60:2=30.

Каждое число можно представить в виде суммы полных десятков и единиц, например: 246=240+6, 1435=1430+5. Так как полные десятки делятся на 5, то и все число делится на б лишь в том случае, когда на б делится число единиц. Это возможно только тогда, когда в разряде единиц стоит цифра О или 5.

Если запись натурального числа оканчивается цифрами О или 5, то это число делится без остатка на 5. Если же запись числа оканчивается иной цифрой, то число без остатка на 5 не делится.

Например, числа 870 и 875 делятся без остатка на 5, а числа 872 и 873 на 5 без остатка не делятся.

Числа, делящиеся без остатка на 2, называют четными, а числа, которые при делении на 2 дают остаток 1, называют нечетными. Из однозначных чисел числа 0, 2, 4, 6 и 8 четны, а числа 1, 3, 5, 7 и 9 нечетны. Поэтому и цифры 0, 2, 4, в, 8 называют четными, а цифры 1, 3, 5, 7, 9 — нечетными.

Все полные десятки делятся на 2 без остатка (.т. е. они четны). Значит, любое натуральное число четно лишь в случае, когда в разряде единиц стоит четная цифра, и нечетно, когда в разряде единиц стоит нечетная цифра.

Если запись натурального числа оканчивается четной цифрой, то это число четно (делится без остатка на 2), а если запись числа оканчивается нечетной цифрой, то это число нечетно.

Например, числа 2, 60, 84, 96, 308 четные, а числа 3, 51, 85, 97, 509 нечетные.

? Как по записи натурального числа определить, делится оно без остатка на 10 или не делится на 10? Как по записи натурального числа узнать, делится оно без остатка на 5 или не делится на 5? Как по записи натурального числа узнать, делится оно без остатка на 2 или не делится на 2?

К 29. Запишите натуральные числа от 1 до 30 в порядке возрастания и подчеркните красным карандашом каждое второе число, а синим — каждое пятое. Какие числа окажутся подчеркнуты красным карандашом, какие — синим? Какие числа подчеркнуты обоими цветами? Назовите числа, не делящиеся ни на 2, ни на 5.

30.    Назовите три числа, которые:

а)    делятся на 2;    в) делятся на 2 и на 5;
б)    делятся на 5;    г) не делятся ни на 2 и ни на 5.

31.    Назовите:

а) два четных числа, кратных 5;
б)    два нечетных числа, кратных 5;
в)    два четных числа, которые не делятся на б;
г)    два нечетных числа, которые не делятся на 5.

32.    Какие из чисел 200, 320, 3000, 60 ООО, 861, 76 540 делятся на 100? Какие из них делятся на 1000? Сформулируйте признаки делимости на 100, на 1000.

33.    Напишите все трехзначные числа, в запись которых могут входить лишь цифры 0, 2, 5 и которые:

а) делятся на 2; б) делятся на 6.

34.    Коля принес несколько коробок с яйцами, по 10 яиц в каждой коробке. Может ли быть, что он принес 32 яйца? 43 яйца? 50 яиц?

35.    Толя купил 2 кг крупы. Может ли его покупка стоить 92 к.? 68 к.? 87 к.?

36.    Купили б кг хлеба. Может ли покупка стоить 92 к.? 90 к.? 75 к.?

37.    Можно ли, используя только цифры 3 и 4, записать:

а)    число, которое делится на 10;           в) число, кратное 5;
б)    четное число;                                    г) нечетное число?

38.    Какие числа, кратные 5, удовлетворяют неравенству:

а) 64<х<78; б) 40б<*<450; в) 24<у<49; г) 1<у<30?

П  39. Вычислите устно:

а) 17+0,3;            б) 0,728-0,7;         в) 0,2-5;      г) 2,6:2;
     0,05+25;             0,8—0,25;           4-2,5;          1,8:9;
     0,37 + 2,03;        1-0,6;                  0,5-20;         3,7:10;
     3,84+0,2;            0,7-0,07;             0,24-1000;    5,3:0,1;

     1,27 + 2,3;          3-0,85;                2,7-100;        6:0,3.

40. Какие различные натуральные числа надо вписать в кружки (рис. 4), чтобы произведение каждых двух чисел, помещенных в кружках, соединенных отрезком, равнялось 70? Подумайте, как можно назвать набор чисел, оказавшихся в кружках.

41.    Если к числу прибавить 4, то полученное число разделится без остатка на 6. Чему равен остаток от деления первого числа на 6?

42.    На микрокалькуляторе по программе получен результат 24.

Попробуйте объяснить, почему получилось такое число. Подумайте, какие числа будут появляться на индикаторе после  каждого нажатия клавиши  при выполнении программы:
 
 
43.    Подтвердите примерами следующее свойство суммы:

а) если каждое слагаемое кратно числу а, то и сумма кратна числу а;

б) если только одно слагаемое суммы не кратно числу а, то сумма не кратна числу а.

44.    Назовите наименьший и наибольший делители числа 24. Назовите наименьшее кратное числу 24. Есть ли у этого числа наибольшее кратное? Назовите какое-нибудь число, кратное и 5 и 12.

45.    Запишите все двузначные числа, являющиеся:

а)    делителями 100;    в) делителями 100 и кратными 25.
б)    кратными 25;

46.    Число b является делителем числа а. Докажите, что частное от деления а на b также является делителем числа а. Проверьте это утверждение, если а=18, a b=3.

47.    Докажите, что:

а)    если а кратно b, а b кратно с, то а кратно с;

б)    если а и b делятся на 6, то и а +  b делится на 6.

48.    Какие из дробей являются правильными и какие неправильными?
49.    При каких натуральных значениях а дробь будет правильной и при каких натуральных значениях b дробь будет неправильной?
50.    Решите уравнение:

 
а)    (х+2,3) • 0,2=0,7;
б)    (2,8-x): 0,3=5;
в)    4,2x + 8,4 = 14,7;
г)    0,39:х-0,1 =0,16.

51. Решите задачу:

Я задумал число. Если его увеличить в 11 раз и результат уменьшить на 2,75, то получится 85,25. Какое число я задумал?
Я задумал число. Если его увеличить на 9,2 и результат увеличить в 11 раз, то получится 110. Какое число я задумал?

Д 52. Найдите среди чисел 154,161, 174,178,191, 315, 320,  346, 425, 475 числа:

а) кратные 2;

б) кратные 5;

в) кратные 10;

г) нечетные.

53.    Напишите:

а)    все четные числа, большие 10 и меньшие 21;
б)    все нечетные числа, большие 12, но меньшие 23.

54.    Напишите три четырехзначных числа, кратные 5.

55.    Выберите из дробей сначала все правильные дроби, а затем неправильные.

56.    Решите уравнение:

а) (4,9 — х):1,2 = 3; б) 3,8•(х-0,2)=2,28.

57.    Найдите значение выражения:

а)    (93-7-1-141):72;                       в) 7091 + 9663—(243 916+ 75 446):527:3;
б)    (357-348:6).4;                          г) 8607+7605+(376012-83 314):414:7.

Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы

_{Математика скачать, задача школьнику 6 класса, материалы по математике для 6 класса онлайн}

Содержание урока
 конспект урока
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.