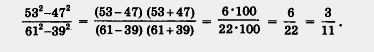Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Что такое разложение многочлена на множители и зачем оно нужно

              Что такое разложение многочлена на множители и зачем оно нужно

Для начала выполним знакомую операцию: умножим многочлен 2х - 3 на многочлен х + 2. Имеем:
(2х - 3) (ч + 2) = 2х • х + 2х • 2 - 3 • х - 3 • 2= 2x² + 4х - Зх - 6 = 2x₂ + х - 6.

Итак, (2х - 3) (х + 2) = 2х² + х- 6.

Это равенство можно записать по-другому, поменяв его части местами:

2x² + х - 6 = (2х - 3) (х + 2).
Такая запись означает, что многочлен 2x² + х - 6 представлен в виде произведения более простых многочленов 2х - 3 и х + 2.

Обычно в таких случаях говорят, что многочлен удалось разложить на множители.

На самом деле термин «разложение многочлена на множители» вам уже знаком, мы несколько раз использовали его в главе 4, но там же мы говорили, что позднее более подробно обсудим эту проблему (проблему разложения многочлена на множители).

Это время пришло. Однако сначала убедимся в том, что разложение многочлена на множители — вещь полезная (иначе зачем нам этим заниматься?).

Представьте себе, что вам предложили решить уравнение 2х - 3 = 0. Вы справитесь с этим без труда: 2х — 3, х — 1,5. Затем вам предложили решить уравнение х + 2 = 0. И с ним вы справитесь легко: х = - 2. Пусть теперь вам предлагают решить уравнение
2x² + х - 6 = 0, т. е. дать ответ на вопрос, при каких значениях х трехчлен 2x² + х - 6 обращается в нуль, — эти значения х обычно называют корнями уравнения. Для таких уравнений имеется специальное правило решения, но вы его пока не знаете. Как быть?

Воспользуемся полученным выше разложением многочлена 2x² + х - 6 на множители: 2x² + х - 6 = (2x - 3) (x + 2). Тогда заданное уравнение можно переписать в виде:

(2x - 3) (x + 2) = 0.

Теперь остается воспользоваться следующим известным фактом: если произведение двух множителей равно нулю, то один из множителей равен нулю. Значит, либо 2x - 3 = 0, либо х + 2 = 0.

Задача свелась к решению двух более простых уравнений. Из уравнения 2x - 3 = 0 получаем x = 1,5. Из уравнения х + 2 = 0 получаем х = - 2. Уравнение решено, оно имеет два корня: 1,5 и - 2.

Итак, разложение многочлена на множители может пригодиться нам для решения уравнений.

Рассмотрим другую ситуацию. Пусть нужно найти значение числового выражения . Самое эффективное решение — дважды воспользоваться формулой разности квадратов:

Разложение на множители позволило нам сократить дробь. Позднее мы оценим это и при выполнении действий с алгебраической дроби.

Таким образом, разложение многочлена на множители используется для решения уравнений, для преобразования числовых и алгебраических выражений. Применяется оно и в других ситуациях, как, скажем, в следующем довольно трудном, но красивом примере, где ключ к успеху опять таки в разложении на множители.

Пример. Доказать, что для любого натурального числа n выражение n³ + Зn² + 2n делится без остатка на 6.

Решение. Пусть р (n) = n³ + Зn² + 2n.
Если n = 1, то р(3) = 1 + 3 + 2 = 6. Значит, р (3) делится на 6 без остатка.
Если n = 2, то р(2) = 2³ + 3•2² + 2•2 = 8 + 12 + 4 = 24. Следовательно, и р(2) делится на 6 без остатка.

Если n = 3, то р(З) = З⁸ + 3•3² + 2•3 = 27 + 27 + 6 = 60.Поэтому и р(3) делится на 6 без остатка.

Но вы же понимаете, что перебрать так все натуральные числа нам не удастся. Как быть? На помощь приходят алгебраические методы.

Имеем:
n³ + Зn² + 2n = n (n + 1) (n + 2).

В самом деле n(n + 1) = n²+ n

a (n²+ n)(n+ 2)=n³+ 2n²+ n²+ 2n=n³+ 3n²+ 2n

Итак,
р(n) = n(n+1)(n + 2),

т. е. р (n) есть произведение трех идущих подряд натуральных чисел n,n + 1,n + 2. Но из трех таких чисел одно обязательно делится на 3, значит, и их произведение делится на 3. Кроме того, по крайней мере одно из этих чисел — четное, т. е. делится на 2, значит, и произведение делится на 2. Итак, р (n) делится и на 2, и на 3, т. е. делится и на 6.

Все прекрасно, скажете вы, но как догадаться, что n³ + Зn² + 2n = n (n + 1) (n + 2)?

Ответ очевиден: надо учиться разложению многочленов на множители. К этому и перейдем: в каждом из следующих параграфов этой главы мы будем изучать тот или иной прием разложения многочлена на множители.

_{Материалы по математике за 7 класс  скачать, конспект по математике , учебники и книги скатать бесплатно, школьная программа онлайн}

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.